Cryptography - ECDSA Algorithm

The Elliptic Curve Digital Signature Algorithm, or ECDSA, is one of the most complex public key cryptography encryption techniques. Elliptic curve cryptography generates smaller keys than digital signature methods. A kind of public key encryption known as elliptic curve cryptography takes advantage of the algebraic structure of elliptic curves over finite fields.

Elliptic curve cryptography is mostly used for creating pseudo-random numbers and digital signatures, among other things. A digital signature is an authentication mechanism that uses a public key pair and a digital certificate to validate the identity of the recipient or sender of information.

What is Elliptic Curve Digital Signature Algorithm?

ECDSA performs the same function as any other digital signature, but more efficiently. This is so that ECDSA, like other digital signature algorithms, can offer the same level of security using smaller keys. ECDSA is used to create ECDSA certificates, which are electronic documents used to authenticate the certificate's owner. Certificates contain information on the key used to create the certificate, the certificate's owner, and the issuer's signature, which is a verified trusted entity.

This trusted issuer is typically a certificate authority with a signed certificate that can be tracked back through the chain of trust to the original issuing certificate authority.

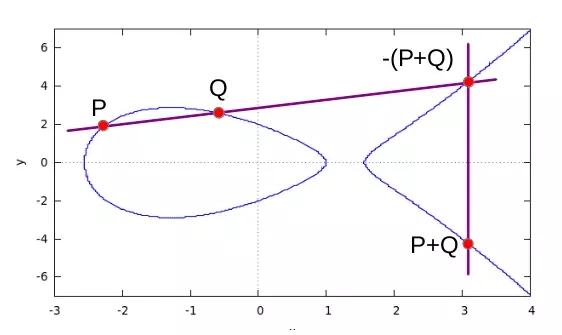
ECDSA operates on elliptic curves by analysing them and selecting a point on the curve. That point is multiplied by another number, resulting in a new point on the curve.

Even with the original point available, locating the new point on the curve is quite challenging. ECDSA's complexity means that it is more secure than current encryption cracking methods. Along with being more secure against current attack methods, ECDSA has a number of additional benefits.

Key and Signature Size

The bit size of the private key considered to be required by ECDSA is approximately two times that of the security level, in bits, similar to elliptic-curve cryptography in general. For example, an ECDSA private key is approximately 160 bits in size at a security level of 80 bits, which needs an attacker to perform a maximum of around 2⁸⁰ operations to discover the private key.

However, the signature size for DSA and ECDSA is the same: approximately 4t bits, where t is the exponent in the formula 2^t for an 80 bit security level, that is, approximately 320 bits, or 2⁸⁰ operations.

Signature Generation

Imagine Alice wants to give Bob a signed message. They have to first agree on the parameters of the curve (CURVE, G, n). G, a base point of prime order on the curve, is required in addition to the field and equation of the curve; n is the multiplicative order of the point G.

Parameter

CURVE − the equation and field for elliptic curves used.
G − base point of an elliptic curve; a point on the curve that produces a big prime order subgroup n.
n − integer order of G, this indicates that n x G = O, where O is the identity element.
d_A − the randomly chosen private key.
Q_A − the key public d_A x G (elliptic curve calculation)
m − the text to be transmitted

The starting point G's order n needs to be prime. In fact, Z/nZ has to be a field because we assume that each nonzero element of the ring is invertible. It means n has to be a prime number.

Alice generates a pair of keys that consist of a public key curve point Q_A = d_A x G and a private key integer d_A, which is chosen at random from the interval [1, n-1]. The elliptic curve point multiplication by a scalar is represented by the symbol x.

Sign a Message

Alice does the following steps in order to sign a message −

Determine e = HASH(m). (Here, HASH refers to a cryptographic hash algorithm that converts the output to an integer, like SHA-2.)
Let z represent the leftmost L_n bits of e, where L_n denotes the group order n bit length. (Take note that z is not longer than n, although it can be.)
Choose k, a random integer that is cryptographically secure, from [1, n-1].
Calculate the curve point where k x G = (x₁, y₁) = 0.
Calculate r by taking x₁ mod n. Refer back to step 3 if r = 0.
S = k^-1 (z + rd_A) mod n, must be calculated. Refer back to step 3 if s = 0.
The pair (r, s) is the signature. In addition, (r, -s mod n) is a valid signature.

An additional method that the ECDSA signature could reveal private keys is if k is produced by an unreliable random number generator. August 2013, users of Android Bitcoin Wallet lost their money due to a random number creation error.

You can produce deterministic signatures by deriving k from the message and the private key, so avoiding random number creation completely and ensuring that k is unique for every communication.

Implementation of ECDSA using Python

So basically we are going to use ecdsa library of python which provides functionality to work with the ECDSA algorithm. And also we will use hashlib library to convert the given message in the hash form. Here is a simple Python implementation of ECDSA with the help of the ecdsa and haslib library −

Example

from ecdsa import SigningKey, VerifyingKey, SECP256k1
import hashlib

# Create a new private key
private_key = SigningKey.generate(curve=SECP256k1)

# Derive the public key from the private key
public_key = private_key.verifying_key

# Some message to sign
message = b"Hello, Tutorialspoint!"

# Hash the message
hash_message = hashlib.sha256(message).digest()

# Sign the hashed message with the private key
signature = private_key.sign(hash_message)

# Verify the signature using the public key
is_valid = public_key.verify(signature, hash_message)

if is_valid:
   print("Signature is valid.")
else:
   print("Signature is not valid.")

Following is the output of the above example −

Input/Output

To run the above code we need to install hashlib and ecdsa libraries of Python. To install these libraries we can use pip install 'libraryName'. So save the code in a file and run this code using python ecdsa_implement.py. Here our file name is ecdsa_implement.py. And the output of the file is as follows −

Signature is valid.

Security of ECDSA

Although RSA is a very secure encryption method, ECC is possibly even more effective.

It is theoretically possible for quantum computers to break RSA by effectively resolving the factoring problem, which is the foundation of RSA. There is a lot of disagreement on when this will occur. It is safe to state, nonetheless, that compared to RSA, ECC is more resilient to quantum computing attacks because of its complexity.

To what extent resistant? In a research paper, a Dutch mathematician, compared breaking cryptographic methods to boiling water. The goal is to determine the energy needed to crack a particular cryptographic algorithm and the volume of water that can be boiled with that energy.

In other words, breaking a 228-bit ECC key can boil all the water on Earth, just cracking a 228-bit RSA key needs less energy than boiling a teaspoon of water. A key size of 2,380 bits is necessary to achieve the same level of security with RSA.

Vulnerabilities of ECDSA

The vulnerability of Elliptic Curve Digital Signature Algorithm, given in the available information, is analysed as follows −

Implementation Complexity − ECDSA is more difficult to implement properly than RSA, which may raise the chance of implementation errors. Poorly implemented Elliptic Curve Digital Signature algorithms can compromise security.
Output Length − ECDSA produces shorter output lengths than RSA for the same level of security. A 3072-bit RSA signature equals the security level of a 256-bit ECDSA signature. Smaller output lengths can make ECDSA signatures more vulnerable to brute-force attacks.
Choice of Elliptic Curves − Elliptic curves are important because some curves allow attackers to brute-force encryption. It is critical to choose elliptic curves that prevent attackers from finding a polynomial-time implementation for the discrete logarithm problem.
Twist Attack − The "twist attack," in which an attacker sends a collection of exactly selected elliptic curve points for the message receiver to cipher, is one potential vulnerability. If the message receiver's algorithm is poorly implemented, the attacker may be able to extract the private key from the ciphertext.
Security vs Implementation Complexity − The difficulty of implementing ECDSA can have an impact on its security. Ensuring secure implementation is critical for avoiding vulnerabilities.

Usage of ECDSA

Secure communication protocols − To enable encryption, digital signatures, and key exchange, ECC is used in a number of secure communication protocols. For example, Virtual Private Networks (VPNs) for secure network communication, Secure Shell (SSH) for secure remote login, and Transport Layer Security (TLS) for safe online browsing.
Blockchain technology and cryptocurrencies − Elliptic curve cryptography is used by several cryptocurrencies, like Bitcoin, Ethereum, and Litecoin, to create public and private key pairs and sign transactions. ECC offers the cryptographic protection needed to protect digital assets and guarantee blockchain network integrity.
Smart cards and embedded systems − ECC is often used to secure electronic passports, payment systems, access control systems, and other applications that call for small, safe cryptographic solutions.

Advantages of ECDSA

A newer standard was established in 2005.
Standardisation decreases hacking time, hence the timeframe is shorter.
Its complexity and newness make it less vulnerable to attacks.
A desirable alternative for emerging protocols for public key cryptography.

Disadvantages of ECDSA

Complex to implement, which can end in incorrect implementations.
With its standardisation in 1995, RSA has a more established history.
Because of its extensive history, RSA remains the most widely used approach.
RSA is easier to set up and has fewer hurdles in deployment.

Print Page