- Cryptography Tutorial
- Cryptography - Home
- Cryptography - Origin
- Cryptography - History
- Cryptography - Principles
- Cryptography - Applications
- Cryptography - Benefits & Drawbacks
- Cryptography - Modern Age
- Cryptography - Traditional Ciphers
- Cryptography - Need for Encryption
- Cryptography - Double Strength Encryption
- Cryptosystems
- Cryptosystems
- Cryptosystems - Components
- Attacks On Cryptosystem
- Cryptosystems - Rainbow table attack
- Cryptosystems - Dictionary attack
- Cryptosystems - Brute force attack
- Cryptosystems - Cryptanalysis Techniques
- Types of Cryptography
- Cryptosystems - Types
- Public Key Encryption
- Modern Symmetric Key Encryption
- Cryptography Hash functions
- Key Management
- Cryptosystems - Key Generation
- Cryptosystems - Key Storage
- Cryptosystems - Key Distribution
- Cryptosystems - Key Revocation
- Block Ciphers
- Cryptosystems - Stream Cipher
- Cryptography - Block Cipher
- Cryptography - Feistel Block Cipher
- Block Cipher Modes of Operation
- Block Cipher Modes of Operation
- Electronic Code Book (ECB) Mode
- Cipher Block Chaining (CBC) Mode
- Cipher Feedback (CFB) Mode
- Output Feedback (OFB) Mode
- Counter (CTR) Mode
- Classic Ciphers
- Cryptography - Reverse Cipher
- Cryptography - Caesar Cipher
- Cryptography - ROT13 Algorithm
- Cryptography - Transposition Cipher
- Cryptography - Encryption Transposition Cipher
- Cryptography - Decryption Transposition Cipher
- Cryptography - Multiplicative Cipher
- Cryptography - Affine Ciphers
- Cryptography - Simple Substitution Cipher
- Cryptography - Encryption of Simple Substitution Cipher
- Cryptography - Decryption of Simple Substitution Cipher
- Cryptography - Vigenere Cipher
- Cryptography - Implementing Vigenere Cipher
- Modern Ciphers
- Base64 Encoding & Decoding
- Cryptography - XOR Encryption
- Substitution techniques
- Cryptography - MonoAlphabetic Cipher
- Cryptography - Hacking Monoalphabetic Cipher
- Cryptography - Polyalphabetic Cipher
- Cryptography - Playfair Cipher
- Cryptography - Hill Cipher
- Polyalphabetic Ciphers
- Cryptography - One-Time Pad Cipher
- Implementation of One Time Pad Cipher
- Cryptography - Transposition Techniques
- Cryptography - Rail Fence Cipher
- Cryptography - Columnar Transposition
- Cryptography - Steganography
- Symmetric Algorithms
- Cryptography - Data Encryption
- Cryptography - Encryption Algorithms
- Cryptography - Data Encryption Standard
- Cryptography - Triple DES
- Cryptography - Double DES
- Advanced Encryption Standard
- Cryptography - AES Structure
- Cryptography - AES Transformation Function
- Cryptography - Substitute Bytes Transformation
- Cryptography - ShiftRows Transformation
- Cryptography - MixColumns Transformation
- Cryptography - AddRoundKey Transformation
- Cryptography - AES Key Expansion Algorithm
- Cryptography - Blowfish Algorithm
- Cryptography - SHA Algorithm
- Cryptography - RC4 Algorithm
- Cryptography - Camellia Encryption Algorithm
- Cryptography - ChaCha20 Encryption Algorithm
- Cryptography - CAST5 Encryption Algorithm
- Cryptography - SEED Encryption Algorithm
- Cryptography - SM4 Encryption Algorithm
- IDEA - International Data Encryption Algorithm
- Public Key (Asymmetric) Cryptography Algorithms
- Cryptography - RSA Algorithm
- Cryptography - RSA Encryption
- Cryptography - RSA Decryption
- Cryptography - Creating RSA Keys
- Cryptography - Hacking RSA Cipher
- Cryptography - ECDSA Algorithm
- Cryptography - DSA Algorithm
- Cryptography - Diffie-Hellman Algorithm
- Data Integrity in Cryptography
- Data Integrity in Cryptography
- Message Authentication
- Cryptography Digital signatures
- Public Key Infrastructure
- Cryptography Useful Resources
- Cryptography - Quick Guide
- Cryptography - Discussion
Cryptography - DSA Algorithm
The Digital Signatures Algorithm is a federal information processing standard for digital signatures. The National Institute of Standards and Technology proposed it in 1991, and it was universally standardised in 1994. It works on the basis of modular exponentiation and discrete logarithmic problems both of which are difficult to solve via brute force.
The following three advantages are offered by the DSA Algorithm −
- Message Authentication − By providing the correct key combination, you can confirm the sender's identity.
- Integrity Verification − Since modifying the message will prevent the bundle from being fully encrypted, it is impossible to tamper with it.
- Non-repudiation − If the signer is verified, the sender cannot argue they never sent the message.
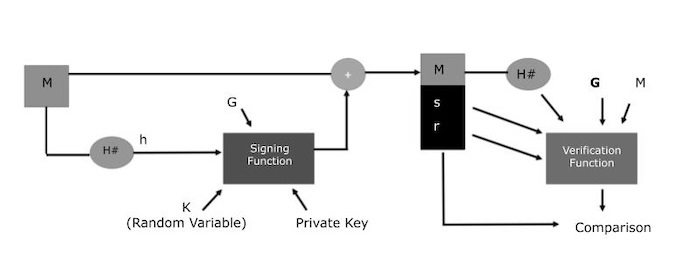
The DSA algorithm's full process can be seen in the diagram above. Here, you will be using two distinct functions: a verification function and a signing function. The encryption and decryption steps are shown in the above image apart from the conventional digital signature verification method. They have different parameters, which you will learn about in the next section below.
How does DSA Work?
Digital Signature Algorithm is what DSA stands for. This cryptographic algorithm is used to protect messages from alteration, create digital signatures, and verify the sender of a digital communication.
Two keys are required for DSA to function: the sender's private key and the recipient's public key.
- The message is signed by the sender using his private key, and it is sent with the message.
- The recipient of the communication then uses the sender's public key to confirm that the signature is authentic and that no tampering has occurred with the message.
- Using special techniques, the verification procedure enables the recipient to verify the signature without needing access to the sender's private key.
Algorithm
Check out how the entire process works check in the image above, from producing the key pair to confirming the signature at the end −
Key Generation
The process of creating keys consists of two steps: per-user keys and parameter generation −
Parameter Generation
- A user must first select a cryptographic hash function (H) and an output length in bits, denoted by |H|. When the output length is longer than |H|, modulus length N is used.
- Then, find a key length L that is a multiple of 64 and ranges between 512 and 1024, as per the original DSS length. However, NIST suggests lengths of 2048 or 3072 for lifetime key security.
- According to FIPS 186-4, the values of L and N must be selected from the following range: (1024, 60), (2048, 224), (2048, 256), or (3072, 256). In addition, while selecting a modulus length N, the user should make sure that it is smaller than the key length (N<L) and equal to the output length (N<=|H|).
- After that, the user can select a prime number (q) of the N bit and another prime number (p) of the L bit so that p-1 is a multiple of q. Next, select an integer, h, from the list (2.....p-2).
- After getting the p and q values, determine − g = h^(p-1)/q*mod(p). Please try a different number for h and compute for g again, excluding 1, if you receive g = 1. The algorithm parameters that are shared by several system users are p, q, and g.
Per-user Keys
The public key, y=g^(x)*mod(p), is calculated after selecting an integer x (the private key) from the list (1.......q-1). This process calculates the key parameters for a particular user.
Signature Generation
- To get our hash digest (h), it runs the original message (M) through the hash function (H#).
- The signing function receives the digest as input and uses two variables, s and r, as output.
- You also use a random integer k, so that 0 < k < q, in addition to the digest.
- Use the formula r = (gk mod p) mod q to find the value of r.
- You can use the formula s = [K - 1(h + x. R)mod q] to find the value of s.
- The signature is then packaged as {r,s}.
- The recipient receives the message and signature bundle in everything ({M, r, s}).
Key Distribution
When distributing keys, a signer has to send the public key (y) to the recipient without using a secret method, publish the private key (x), and keep it a secret.
Signing
The correct way to sign message m is as follows −
- First, select an integer k from the (1.......q-1) and
- Compute: r = g^(k)*mod(p)*mod(q). Try a different random value for k and compute again for all values of r excluding 0. If you get r = 0.
- Calculate: s=(k^(-1)*(H(m)+xr))*mod(q). Please try another random value for k and compute again for all values of s excluding 0. If you get s = 0.
- Two key elements define the signature (r,s). Also, a new message is created using key elements k and r. But calculating r using the modular exponential method is a very costly process that has to be done before the message is received.
Signature Verification
- To create the digest h, you use a similar hash function (H#).
- The verification function then receives this digest and needs additional variables as input.
- Calculate the value of w so that it s*w mod q equals one.
- Determine u1's value using the formula u1 = h*w mod q.
- Use the formula u2 = r*w mod q to figure out the value of u2.
- The formula for calculating the final verification component, v, is v = [((gu1. yu2) mod p) mod q].
- The value of v is compared to the value of r that was received in the bundle.
- The signature verification process is finished if they match.
How is Sender Authenticated by the Algorithm?
By confirming the digital signature of the communication, the algorithm verifies the sender's identity.
- The sender's private key, which is unique to them, is used to create the digital signature.
- The digital signature is then verified by the recipient using the sender's public key.
- The recipient will know the sender transmitted the message if the digital signature is legitimate.
Advantages of DSA
See the advantages of DSA below −
- When compared to other signature verification techniques, DSA is extremely robust in terms of security and stability.
- Compared to other algorithms like the RSA algorithm, the key creation is considerably faster.
- DSA uses less space in storage to run its full cycle.
- When NIST released it, it was free of patents to allow for its free worldwide use.
Disadvantages of DSA
One of the most widely used algorithms for digital signature creation is DSA. DSA, however, may have some drawbacks.
- The usage of DSA has limitations to particular applications because of its limited key lengths.
- Limited key lengths are needed for rigid key management.
- DSA can only be used in a limited number of applications because it does not support certificates.
- DSA cannot be modified or modified after a signature is generated since it is not an incremental signature algorithm.
- Unlike some of the more well-established algorithms, DSA is a relatively new algorithm and has not undergone considerable research or testing.
- DSA signatures have a tendency to be larger than signatures produced by other algorithms, which can decrease the effectiveness of transmission and storage.
Advertisements