
- MATLAB - Home
- MATLAB - Overview
- MATLAB - Features
- MATLAB - Environment Setup
- MATLAB - Editors
- MATLAB - Online
- MATLAB - Workspace
- MATLAB - Syntax
- MATLAB - Variables
- MATLAB - Commands
- MATLAB - Data Types
- MATLAB - Operators
- MATLAB - Dates and Time
- MATLAB - Numbers
- MATLAB - Random Numbers
- MATLAB - Strings and Characters
- MATLAB - Text Formatting
- MATLAB - Timetables
- MATLAB - M-Files
- MATLAB - Colon Notation
- MATLAB - Data Import
- MATLAB - Data Output
- MATLAB - Normalize Data
- MATLAB - Predefined Variables
- MATLAB - Decision Making
- MATLAB - Decisions
- MATLAB - If End Statement
- MATLAB - If Else Statement
- MATLAB - If…Elseif Else Statement
- MATLAB - Nest If Statememt
- MATLAB - Switch Statement
- MATLAB - Nested Switch
- MATLAB - Loops
- MATLAB - Loops
- MATLAB - For Loop
- MATLAB - While Loop
- MATLAB - Nested Loops
- MATLAB - Break Statement
- MATLAB - Continue Statement
- MATLAB - End Statement
- MATLAB - Arrays
- MATLAB - Arrays
- MATLAB - Vectors
- MATLAB - Transpose Operator
- MATLAB - Array Indexing
- MATLAB - Multi-Dimensional Array
- MATLAB - Compatible Arrays
- MATLAB - Categorical Arrays
- MATLAB - Cell Arrays
- MATLAB - Matrix
- MATLAB - Sparse Matrix
- MATLAB - Tables
- MATLAB - Structures
- MATLAB - Array Multiplication
- MATLAB - Array Division
- MATLAB - Array Functions
- MATLAB - Functions
- MATLAB - Functions
- MATLAB - Function Arguments
- MATLAB - Anonymous Functions
- MATLAB - Nested Functions
- MATLAB - Return Statement
- MATLAB - Void Function
- MATLAB - Local Functions
- MATLAB - Global Variables
- MATLAB - Function Handles
- MATLAB - Filter Function
- MATLAB - Factorial
- MATLAB - Private Functions
- MATLAB - Sub-functions
- MATLAB - Recursive Functions
- MATLAB - Function Precedence Order
- MATLAB - Map Function
- MATLAB - Mean Function
- MATLAB - End Function
- MATLAB - Error Handling
- MATLAB - Error Handling
- MATLAB - Try...Catch statement
- MATLAB - Debugging
- MATLAB - Plotting
- MATLAB - Plotting
- MATLAB - Plot Arrays
- MATLAB - Plot Vectors
- MATLAB - Bar Graph
- MATLAB - Histograms
- MATLAB - Graphics
- MATLAB - 2D Line Plot
- MATLAB - 3D Plots
- MATLAB - Formatting a Plot
- MATLAB - Logarithmic Axes Plots
- MATLAB - Plotting Error Bars
- MATLAB - Plot a 3D Contour
- MATLAB - Polar Plots
- MATLAB - Scatter Plots
- MATLAB - Plot Expression or Function
- MATLAB - Draw Rectangle
- MATLAB - Plot Spectrogram
- MATLAB - Plot Mesh Surface
- MATLAB - Plot Sine Wave
- MATLAB - Interpolation
- MATLAB - Interpolation
- MATLAB - Linear Interpolation
- MATLAB - 2D Array Interpolation
- MATLAB - 3D Array Interpolation
- MATLAB - Polynomials
- MATLAB - Polynomials
- MATLAB - Polynomial Addition
- MATLAB - Polynomial Multiplication
- MATLAB - Polynomial Division
- MATLAB - Derivatives of Polynomials
- MATLAB - Transformation
- MATLAB - Transforms
- MATLAB - Laplace Transform
- MATLAB - Laplacian Filter
- MATLAB - Laplacian of Gaussian Filter
- MATLAB - Inverse Fourier transform
- MATLAB - Fourier Transform
- MATLAB - Fast Fourier Transform
- MATLAB - 2-D Inverse Cosine Transform
- MATLAB - Add Legend to Axes
- MATLAB - Object Oriented
- MATLAB - Object Oriented Programming
- MATLAB - Classes and Object
- MATLAB - Functions Overloading
- MATLAB - Operator Overloading
- MATLAB - User-Defined Classes
- MATLAB - Copy Objects
- MATLAB - Algebra
- MATLAB - Linear Algebra
- MATLAB - Gauss Elimination
- MATLAB - Gauss-Jordan Elimination
- MATLAB - Reduced Row Echelon Form
- MATLAB - Eigenvalues and Eigenvectors
- MATLAB - Integration
- MATLAB - Integration
- MATLAB - Double Integral
- MATLAB - Trapezoidal Rule
- MATLAB - Simpson's Rule
- MATLAB - Miscellenous
- MATLAB - Calculus
- MATLAB - Differential
- MATLAB - Inverse of Matrix
- MATLAB - GNU Octave
- MATLAB - Simulink
MATLAB - Graphics
This chapter will continue exploring the plotting and graphics capabilities of MATLAB. We will discuss −
- Drawing bar charts
- Drawing contours
- Three dimensional plots
Drawing Bar Charts
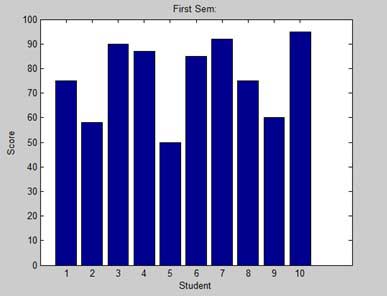
The bar command draws a two dimensional bar chart. Let us take up an example to demonstrate the idea.
Example
Let us have an imaginary classroom with 10 students. We know the percent of marks obtained by these students are 75, 58, 90, 87, 50, 85, 92, 75, 60 and 95. We will draw the bar chart for this data.
Create a script file and type the following code −
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps
When you run the file, MATLAB displays the following bar chart −
Drawing Contours
A contour line of a function of two variables is a curve along which the function has a constant value. Contour lines are used for creating contour maps by joining points of equal elevation above a given level, such as mean sea level.
MATLAB provides a contour function for drawing contour maps.
Example
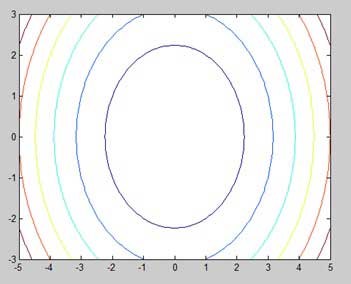
Let us generate a contour map that shows the contour lines for a given function g = f(x, y). This function has two variables. So, we will have to generate two independent variables, i.e., two data sets x and y. This is done by calling the meshgrid command.
The meshgrid command is used for generating a matrix of elements that give the range over x and y along with the specification of increment in each case.
Let us plot our function g = f(x, y), where 5 x 5, 3 y 3. Let us take an increment of 0.1 for both the values. The variables are set as −
[x,y] = meshgrid(5:0.1:5, 3:0.1:3);
Lastly, we need to assign the function. Let our function be: x2 + y2
Create a script file and type the following code −
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function contour(x,y,g) % call the contour function print -deps graph.eps
When you run the file, MATLAB displays the following contour map −
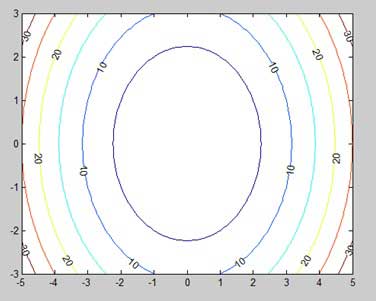
Let us modify the code a little to spruce up the map
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function [C, h] = contour(x,y,g); % call the contour function set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2) print -deps graph.eps
When you run the file, MATLAB displays the following contour map −
Three Dimensional Plots
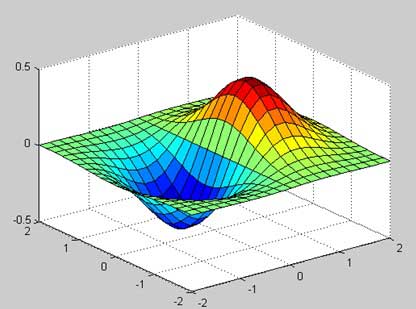
Three-dimensional plots basically display a surface defined by a function in two variables, g = f (x,y).
As before, to define g, we first create a set of (x,y) points over the domain of the function using the meshgrid command. Next, we assign the function itself. Finally, we use the surf command to create a surface plot.
The following example demonstrates the concept −
Example
Let us create a 3D surface map for the function g = xe-(x2 + y2)
Create a script file and type the following code −
[x,y] = meshgrid(-2:.2:2); g = x .* exp(-x.^2 - y.^2); surf(x, y, g) print -deps graph.eps
When you run the file, MATLAB displays the following 3-D map −
You can also use the mesh command to generate a three-dimensional surface. However, the surf command displays both the connecting lines and the faces of the surface in color, whereas, the mesh command creates a wireframe surface with colored lines connecting the defining points.