Prolog - Tree Data Structure (Case Study)

So far we have seen different concepts of logic programming in Prolog. Now we will see one case study on Prolog. We will see how to implement a tree data structure using Prolog, and we will create our own operators. So let us start the planning.

Suppose we have a tree as shown below −

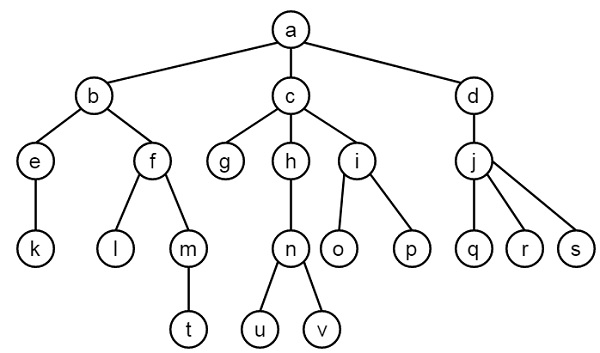
We have to implement this tree using prolog. We have some operations as follows −

• op(500, xfx, 'is_parent').

• op(500, xfx, 'is_sibling').

• op(500, xfx, 'is_at_same_level').

• And another predicate namely leaf_node(Node)

In these operators, you have seen some parameters as (500, xfx, <operator_name>). The first argument (here 500) is the priority of that operator. The xfx indicates that this is a binary operator and the <operator_name> is the name of the operator.

These operators can be used to define the tree database. We can use these operators as follows −

• a is_parent b, or is_parent(a, b). So this indicates that node a is the parent of node b.

• X is_sibling_of Y or is_sibling_of(X,Y). This indicates that X is the sibling of node Y. So the rule is, if another node Z is parent of X and Z is also the parent of Y and X and Y are different, then X and Y are siblings.

• leaf_node(Node). A node (Node) is said to be a leaf node when a node has no children.

• X is_at_same_level Y, or is_at_same_level(X,Y). This will check whether X and Y are at the same level or not. So the condition is when X and Y are same, then it returns true, otherwise W is the parent of X, Z is the parent of Y and W and Z are at the same level.

As shown above, other rules are defined in the code. So let us see the program to get better view.

Program (case_tree.pl)

/* The tree database */:- op(500,xfx,'is_parent').
a is_parent b. 
c is_parent g. 
f is_parent l. 
j is_parent q.
a is_parent c. 
c is_parent h. 
f is_parent m. 
j is_parent r.
a is_parent d. 
c is_parent i. 
h is_parent n. 
j is_parent s.
b is_parent e. 
d is_parent j. 
i is_parent o. 
m is_parent t.
b is_parent f. 
e is_parent k. 
i is_parent p. 
n is_parent u.
n is_parent v.
/* X and Y are siblings i.e. child from the same parent */:- op(500,xfx,'is_sibling_of').
X is_sibling_of Y :- Z is_parent X, Z is_parent Y, X \== Y.
leaf_node(Node) :- \+ is_parent(Node,Child). % Node grounded
/* X and Y are on the same level in the tree. */:- op(500,xfx,'is_at_same_level').
X is_at_same_level X.
X is_at_same_level Y :- W is_parent X, Z is_parent Y,W is_at_same_level Z.

Output

| ?- consult('D:/TP Prolog/Sample Codes/case_tree.pl').
compiling D:/TP Prolog/Sample Codes/case_tree.pl for byte code...
D:/TP Prolog/Sample Codes/case_tree.pl:25: warning: singleton variables [Child] for leaf_node/1
D:/TP Prolog/Sample Codes/case_tree.pl compiled, 27 lines read - 3244 bytes written, 4 ms

(31 ms) yes
| ?- i is_parent p.

yes
| ?- i is_parent s.

no
| ?- is_parent(i,p).

yes
| ?- e is_sibling_of f.

true ? 

yes
| ?- is_sibling_of(e,g).

no
| ?- leaf_node(v).

yes
| ?- leaf_node(a).

no
| ?- is_at_same_level(l,s).

true ? 

yes
| ?- l is_at_same_level v.

no
| ?- 

More Tree Operations

Advances in Tree Data Structures