Prolog - Recursion and Structures

---

---

This chapter covers recursion and structures.

Recursion

Recursion is a technique in which one predicate uses itself (may be with some other predicates) to find the truth value.

Let us understand this definition with the help of an example −

is_digesting(X,Y) :- just_ate(X,Y).
is_digesting(X,Y) :-just_ate(X,Z),is_digesting(Z,Y).

So this predicate is recursive in nature. Suppose we say that just_ate(deer, grass), it means is_digesting(deer, grass) is true. Now if we say is_digesting(tiger, grass), this will be true if is_digesting(tiger, grass) :- just_ate(tiger, deer), is_digesting(deer, grass), then the statement is_digesting(tiger, grass) is also true.

There may be some other examples also, so let us see one family example. So if we want to express the predecessor logic, that can be expressed using the following diagram −

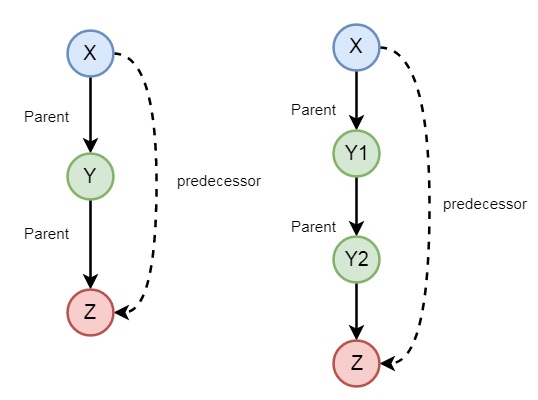
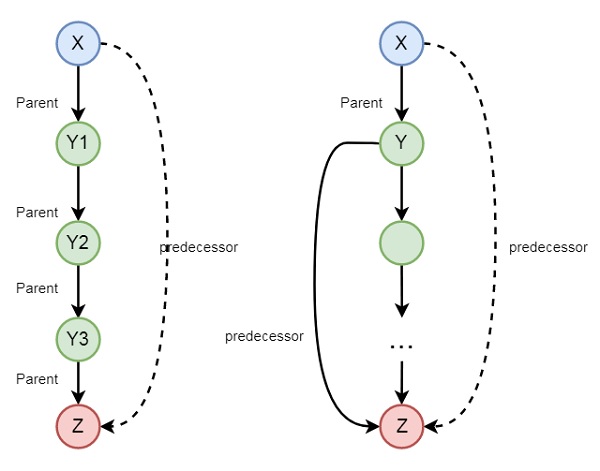
So we can understand the predecessor relationship is recursive. We can express this relationship using the following syntax −

predecessor(X, Z) :- parent(X, Z).
predecessor(X, Z) :- parent(X, Y),predecessor(Y, Z).

Now let us see the practical demonstration −

recursive.pl

female(pam).
female(liz).
female(pat).
female(ann).
male(jim).
male(bob).
male(tom).
male(peter).
parent(pam,bob).
parent(tom,bob).
parent(tom,liz).
parent(bob,ann).
parent(bob,pat).
parent(pat,jim).
parent(bob,peter).
parent(peter,jim).
mother(X,Y):- parent(X,Y),female(X).
father(X,Y):- parent(X,Y),male(X).
haschild(X):- parent(X,_).
sister(X,Y):- parent(Z,X),parent(Z,Y),female(X),X\==Y.
brother(X,Y):-parent(Z,X),parent(Z,Y),male(X),X\==Y.
predecessor(X, Z) :- parent(X, Z).
predecessor(X, Z) :- parent(X, Y),predecessor(Y, Z).

Output

| ?- consult('D:/TP Prolog/Sample Codes/recursive.pl').
compiling D:/TP Prolog/Sample Codes/recursive.pl for byte code...
D:/TP Prolog/Sample Codes/recursive.pl compiled, 22 lines read - 3486 bytes written, 7 ms

(47 ms) yes
| ?- predecessor(X, jim).

X = pat ? 

yes
| ?- 

Structures

Structures are Data Objects that contain multiple components.

For example, the date can be viewed as a structure with three components day, month and year. Then the date 9th April, 2020 can be written as: date(9, apr, 2020).

Note − Structure can in turn have another structure as a component in it.

So we can see views as tree structure and Prolog Functors.

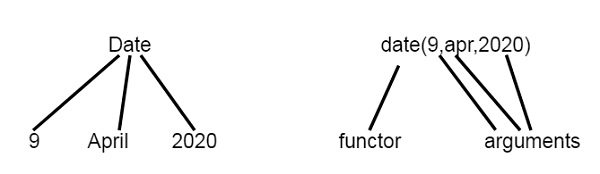
Now let us see one example of structures in Prolog. We will define a structure of points, Segments and Triangle as structures.

To represent a point, a line segment and a triangle using structure in Prolog, we can consider following statements −

• p1 − point(1, 1)

• p2 − point(2,3)

• S − seg( Pl, P2): seg( point(1,1), point(2,3))

• T − triangle( point(4,Z), point(6,4), point(7,1) )

Note − Structures can be naturally pictured as trees. Prolog can be viewed as a language for processing trees.

Matching in Prolog

Matching is used to check whether two given terms are same (identical) or the variables in both terms can have the same objects after being instantiated. Let us see one example.

Suppose date structure is defined as date(D,M,2020) = date(D1,apr, Y1), this indicates that D = D1, M = feb and Y1 = 2020.

Following rules are to be used to check whether two terms S and T match −

• If S and T are constants, S=T if both are same objects.

• If S is a variable and T is anything, T=S.

• If T is variable and S is anything, S=T.

• If S and T are structures, S=T if −

  • S and T have same functor.

  • All their corresponding arguments components have to match.

Binary Trees

Following is the structure of binary tree using recursive structures −

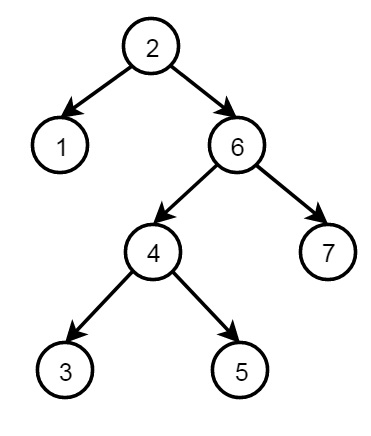
The definition of the structure is as follows −

node(2, node(1,nil,nil), node(6, node(4,node(3,nil,nil), node(5,nil,nil)), node(7,nil,nil))

Each node has three fields, data and two nodes. One node with no child (leaf node) structure is written as node(value, nil, nil), node with only one left child is written as node(value, left_node, nil), node with only one right child is written as node(value, nil; right_node), and node with both child has node(value, left_node, right_node).