DSP - In-Place Computation

---

---

This efficient use of memory is important for designing fast hardware to calculate the FFT. The term in-place computation is used to describe this memory usage.

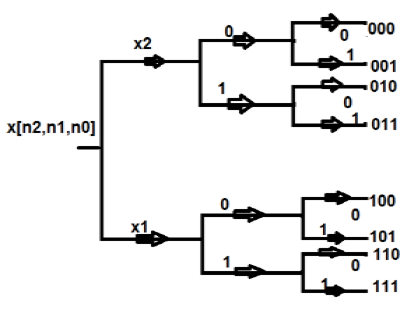
Decimation in Time Sequence

In this structure, we represent all the points in binary format i.e. in 0 and 1. Then, we reverse those structures. The sequence we get after that is known as bit reversal sequence. This is also known as decimation in time sequence. In-place computation of an eight-point DFT is shown in a tabular format as shown below −

Decimation in Frequency Sequence

Apart from time sequence, an N-point sequence can also be represented in frequency. Let us take a four-point sequence to understand it better.

Let the sequence be $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. We will group two points into one group, initially. Mathematically, this sequence can be written as;

$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$

Now let us make one group of sequence number 0 to 3 and another group of sequence 4 to 7. Now, mathematically this can be shown as;

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$

Let us replace n by r, where r = 0, 1 , 2.(N/2-1). Mathematically,

$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$

We take the first four points (x[0], x[1], x[2], x[3]) initially, and try to represent them mathematically as follows −

$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$

$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$

now $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$

$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$

$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$

We can further break it into two more parts, which means instead of breaking them as 4-point sequence, we can break them into 2-point sequence.