
- SciPy - Home
- SciPy - Introduction
- SciPy - Environment Setup
- SciPy - Basic Functionality
- SciPy - Relationship with NumPy
- SciPy Clusters
- SciPy - Clusters
- SciPy - Hierarchical Clustering
- SciPy - K-means Clustering
- SciPy - Distance Metrics
- SciPy Constants
- SciPy - Constants
- SciPy - Mathematical Constants
- SciPy - Physical Constants
- SciPy - Unit Conversion
- SciPy - Astronomical Constants
- SciPy - Fourier Transforms
- SciPy - FFTpack
- SciPy - Discrete Fourier Transform (DFT)
- SciPy - Fast Fourier Transform (FFT)
- SciPy Integration Equations
- SciPy - Integrate Module
- SciPy - Single Integration
- SciPy - Double Integration
- SciPy - Triple Integration
- SciPy - Multiple Integration
- SciPy Differential Equations
- SciPy - Differential Equations
- SciPy - Integration of Stochastic Differential Equations
- SciPy - Integration of Ordinary Differential Equations
- SciPy - Discontinuous Functions
- SciPy - Oscillatory Functions
- SciPy - Partial Differential Equations
- SciPy Interpolation
- SciPy - Interpolate
- SciPy - Linear 1-D Interpolation
- SciPy - Polynomial 1-D Interpolation
- SciPy - Spline 1-D Interpolation
- SciPy - Grid Data Multi-Dimensional Interpolation
- SciPy - RBF Multi-Dimensional Interpolation
- SciPy - Polynomial & Spline Interpolation
- SciPy Curve Fitting
- SciPy - Curve Fitting
- SciPy - Linear Curve Fitting
- SciPy - Non-Linear Curve Fitting
- SciPy - Input & Output
- SciPy - Input & Output
- SciPy - Reading & Writing Files
- SciPy - Working with Different File Formats
- SciPy - Efficient Data Storage with HDF5
- SciPy - Data Serialization
- SciPy Linear Algebra
- SciPy - Linalg
- SciPy - Matrix Creation & Basic Operations
- SciPy - Matrix LU Decomposition
- SciPy - Matrix QU Decomposition
- SciPy - Singular Value Decomposition
- SciPy - Cholesky Decomposition
- SciPy - Solving Linear Systems
- SciPy - Eigenvalues & Eigenvectors
- SciPy Image Processing
- SciPy - Ndimage
- SciPy - Reading & Writing Images
- SciPy - Image Transformation
- SciPy - Filtering & Edge Detection
- SciPy - Top Hat Filters
- SciPy - Morphological Filters
- SciPy - Low Pass Filters
- SciPy - High Pass Filters
- SciPy - Bilateral Filter
- SciPy - Median Filter
- SciPy - Non - Linear Filters in Image Processing
- SciPy - High Boost Filter
- SciPy - Laplacian Filter
- SciPy - Morphological Operations
- SciPy - Image Segmentation
- SciPy - Thresholding in Image Segmentation
- SciPy - Region-Based Segmentation
- SciPy - Connected Component Labeling
- SciPy Optimize
- SciPy - Optimize
- SciPy - Special Matrices & Functions
- SciPy - Unconstrained Optimization
- SciPy - Constrained Optimization
- SciPy - Matrix Norms
- SciPy - Sparse Matrix
- SciPy - Frobenius Norm
- SciPy - Spectral Norm
- SciPy Condition Numbers
- SciPy - Condition Numbers
- SciPy - Linear Least Squares
- SciPy - Non-Linear Least Squares
- SciPy - Finding Roots of Scalar Functions
- SciPy - Finding Roots of Multivariate Functions
- SciPy - Signal Processing
- SciPy - Signal Filtering & Smoothing
- SciPy - Short-Time Fourier Transform
- SciPy - Wavelet Transform
- SciPy - Continuous Wavelet Transform
- SciPy - Discrete Wavelet Transform
- SciPy - Wavelet Packet Transform
- SciPy - Multi-Resolution Analysis
- SciPy - Stationary Wavelet Transform
- SciPy - Statistical Functions
- SciPy - Stats
- SciPy - Descriptive Statistics
- SciPy - Continuous Probability Distributions
- SciPy - Discrete Probability Distributions
- SciPy - Statistical Tests & Inference
- SciPy - Generating Random Samples
- SciPy - Kaplan-Meier Estimator Survival Analysis
- SciPy - Cox Proportional Hazards Model Survival Analysis
- SciPy Spatial Data
- SciPy - Spatial
- SciPy - Special Functions
- SciPy - Special Package
- SciPy Advanced Topics
- SciPy - CSGraph
- SciPy - ODR
- SciPy Useful Resources
- SciPy - Reference
- SciPy - Quick Guide
- SciPy - Cheatsheet
- SciPy - Useful Resources
- SciPy - Discussion
Scipy - Integrate
SciPy's Integrate module provides functions for performing numerical integration, allowing users to compute both definite and indefinite integrals of mathematical functions. It includes various methods suitable for different types of integration tasks such as single-variable, double and triple integrals.
The Key functions of Integrate module such as quad for single integrals, dblquad for double integrals, tplquad for triple integrals and odeint for solving ordinary differential equations.
This module is widely used in fields like physics, engineering, statistics and economics to analyze continuous data which compute areas under curves and solve dynamic systems.
Key Functions in SciPy Integrate Module
The scipy.integrate module offers several key functions for performing numerical integration and solving ordinary differential equations (ODEs). Here are some of the most important functions −
SciPy Integration Module
The scipy.integrate module provides various methods to perform the operation of numerical integration. Following are the list of methods to understand its functionality −
| Sr.No. | Types & Description |
|---|---|
| 1 |
This method is used to perform the task of definite integrals. |
| 2 |
This method is used to calculate the definite integrals of vector-value function. |
| 3 |
This is used to calculate the double numerical integration. |
| 4 |
This method is used to calculate the triple numerical integration. |
| 5 |
This method is used to find the integration of multiple variable. |
| 6 |
This method operates the fixed order of Gaussian quadrature for numerical integration. |
| 7 |
This method is used to calculate the numerical integration. |
| 8 |
This method is used to calculate the numerical integration. |
| 9 |
This method is used to return the weights and error coefficient for Newton-Cotes integration. |
| 10 |
This method is used to find the approximate value of integral function using trapezoid rule. |
| 11 |
integrate.cumulative_trapezoid() This method is used to calculate the integral from the given set of points using trapezoidal rule. |
| 12 |
This method is used to approximate the integral of a function using Simpson rule. |
| 13 |
integrate.cumulative_simpson() This method is used to calculate the coordinates at every pairs |
| 14 |
This method is used to perform the task of numerical or romberg integration. |
Key Features of Scipy Integrate Module
The scipy.integrate module provides various features for numerical integration and solving differential equations. Below are some key features −
- Adaptive Quadrature: Functions such as quad utilize adaptive algorithms to efficiently estimate integrals by dynamically adjusting the number of evaluation points based on the function's behavior.
- Support for Multidimensional Integration: Functions such as dblquad and tplquad are used to enable the computation of double and triple integrals over specified regions by making it easy to handle higher-dimensional problems.
- Integration of Ordinary Differential Equations (ODEs): This module includes functions such as odeint and solve_ivp, which are designed to solve initial value problems for ordinary differential equations using various methods including adaptive algorithms.
- Flexible Input: Users can specify custom functions for integration and differential equations by allowing for a wide variety of mathematical models to be analyzed.
- Time Integration: The solve_ivp function provides various integration methods such as Runge-Kutta and implicit methods to handle stiff and non-stiff ODEs effectively.
- Event Handling: The solve_ivp function supports event detection by allowing users to specify conditions under which the integration should stop or change behavior.
- Robust Error Handling: These functions provide error estimates and warnings for integration problems by helping users identify potential issues with the integration process.
- High Performance: The underlying algorithms are optimized for speed and accuracy by making scipy.integrate suitable for both simple and complex numerical integration tasks.
These features make scipy.integrate module a powerful and flexible tool for numerical analysis in scientific computing and engineering applications.
Applications
Below are the applications of the Scipy Integrate module in various Fields −
- Physics and Engineering: This module is used for solving problems involving areas, volumes and forces.
- Probability and Statistics: The scipy Integrate module is used for computing probabilities and expected values in continuous distributions.
- Economics: This module helps in integrating utility functions and other models over continuous ranges.
Example
Here's an example showing how to use the scipy.integrate module for both numerical integration and solving ordinary differential equations (ODEs) −
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
# Example 1: Numerical Integration
# Define the function to be integrated
def f(x):
return np.sin(x)
# Perform the integration of f from 0 to p
integral_result, error = integrate.quad(f, 0, np.pi)
print(f"Numerical Integration Result: {integral_result}")
print(f"Estimated Error: {error}")
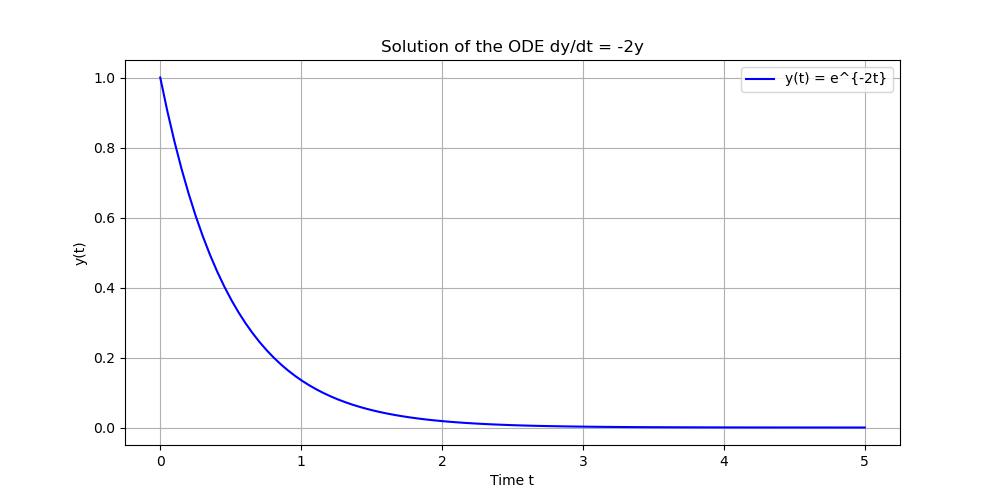
# Example 2: Solving an Ordinary Differential Equation
# Define the ODE dy/dt = -2y
def model(y, t):
return -2 * y
# Initial condition
y0 = 1
# Time points where solution is computed
t = np.linspace(0, 5, 100)
# Solve the ODE
solution = integrate.odeint(model, y0, t)
# Plotting the results
plt.figure(figsize=(10, 5))
plt.plot(t, solution, label='y(t) = e^{-2t}', color='blue')
plt.title('Solution of the ODE dy/dt = -2y')
plt.xlabel('Time t')
plt.ylabel('y(t)')
plt.legend()
plt.grid()
plt.show()
Below is the output of the scipy Integrate module which is used to calculate the numerical Integration −
Numerical Integration Result: 2.0 Estimated Error: 2.220446049250313e-14