Plotting rational numbers on a number line

A rational number is a fraction and is plotted on a number line as follows.

Basic rules of representing rational no. on number line

• If the rational no.(fraction) is proper then, it lies between 0 and 1.

• If the rational no.(fraction) is improper then, we first convert it to mixed fraction and then the given rational no. lies between the whole number and next whole number.

We use following steps to represent a rational number or fraction for example, $\frac{5}{7}$ on the number line.

Step 1 − We draw a number line.

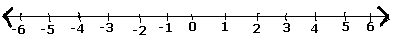
Step 2 − As the number $\frac{5}{7}$ is a positive number, it lies on the right side of zero.

Step 3 − So, after zero mark, we have $\frac{1}{7}, \: \frac{2}{7}, \: \frac{3}{7}, \: \frac{4}{7}, \: \frac{5}{7}, \: \frac{6}{7},$ and ($\frac{7}{7}$ = 1).

Step 4 − The rational number $\frac{5}{7}$ on the number line is shown as follows.

Plot $\frac{1}{4}$ and $1\frac{2}{4}$ on the number line below

Solution

Step 1:

$\frac{1}{4}$(A) lies between 0 and 1; $1\frac{2}{4}$ (B)lies between 1 and 2

Step 2:

Each division is divided into four parts as the bottom of the fractions is 4.

$\frac{1}{4}$ is the first mark after 0, therefore point A represents $\frac{1}{4}$

$1\frac{2}{4}$ is the second mark after 1, so point B represents $1\frac{2}{4}$

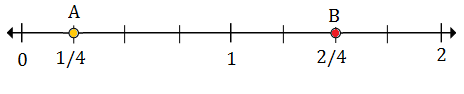
Plot $\frac{5}{8}$ and $2\frac{3}{8}$ on the number line below

Solution

Step 1:

$\frac{5}{8}$ 8 (A) lies between 0 and 1; $2\frac{3}{8}$ (B)lies between 2 and 3

Step 2:

Each division is divided into eight parts as the bottom of the fractions is 8.

$\frac{5}{8}$ is the fifth mark after 0, therefore point A represents $\frac{5}{8}$

$2\frac{3}{8}$ is the third mark after 2, so point B represents $2\frac{3}{8}$