
- Matlab-Matrix Tutorial
- Matlab-Matrix - Home
- Matlab-Matrix - Introduction
- Matlab-Matrix - Environment Setup
- Matlab-Matrix - Create Matrix
- Matlab-Matrix - Working with Matrices
- Matlab-Matrix - Multiplication
- Matlab-Matrix - Addition
- Matlab-Matrix - Subtraction
- Matlab-Matrix - Matrix Determinant
- Matlab-Matrix - Inverse
- Matlab-Matrix - Trace
- Matlab-Matrix - Rank
- Matlab-Matrix - Transpose
- Matlab-Matrix - Deletion Row & Coloumn
- Matlab-Matrix Useful Resources
- Matlab Matrix - Quick Guide
- Matlab Matrix - Useful Resources
- Matlab Matrix - Discussion
Matlab-Matrix - Introduction
MATLAB (matrix laboratory) is a fourth-generation high-level programming language and interactive environment for numerical computation, visualization and programming. It allows matrix manipulations; plotting of functions and data; implementation of algorithms; creation of user interfaces; interfacing with programs written in other languages, including C, C++, Java, and FORTRAN; analyze data; develop algorithms; and create models and applications.
In this tutorial we will focus on Matrix Implementation using MATLAB.
Matrix
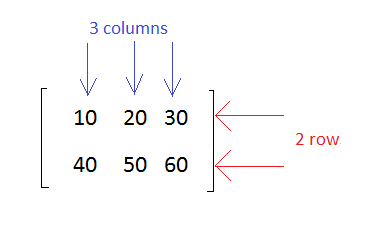
A matrix is a collection of numbers arranged in rows and columns that represents a rectangular array.
An example of matrix with 2 rows and 3 columns is as shown below
Matrix Dimension
The dimension of a matrix is defined based on the number of rows and columns.
A matrix with 2 rows and 3 columns is said to be 2x3 matrix.
A matrix with 3 rows and 3 columns is said to be 3x3 matrix.
Matrix in Matlab
In MATLAB, you create a matrix by entering elements in each row as comma or space delimited numbers and using semicolons to mark the end of each row.
Example
To create a 4x5 matrix, enter the following.
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]
The matrix has 4 rows and 5 columns.
The first row will have values as 1 2 3 4 5
The second row: 2 3 4 5 6
The third row: 3 4 5 6 7
The fourth row: 4 5 6 7 8
Output
The matrix of size 4x5 will look as follows
a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8
Let us test the matrix creation in MATLAB command window as shown below −
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >>
Referencing the Elements
To reference an element in the mth row and nth column, of a matrix mx, we write the following
mx(m, n);
Example
To refer to the element in the 2nd row and 5th column, of the matrix a, as created in the last section, we type the following.
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> a(2,5) ans = 6 >>
To get all the elements of the nth column in a matrix , you can make use of A (:,n) where n represents the column no in the matrix.
A(:,n).
Example
Now, let us create a column vector v, from all the elements of the 4th column of the matrix a. This will be as follows
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; v = a(:,4)
Output
MATLAB will execute the above statement and return the following result.
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> v=a(:,4) v = 4 5 6 7 >>
You can also select the elements in the mth through nth columns. For this, we write as follows.
a(:,m:n)
Example
Let us create a smaller matrix by taking the elements from the second and third columns, as shown below −
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
Output
MATLAB will execute the above statement and return the following result −
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> a(:, 2:3) ans = 2 3 3 4 4 5 5 6 >>
In the same way, you can create a sub-matrix by taking a sub-part of a matrix.
Example
Let us create a sub-matrix saby taking the inner subpart of a, as given below −
3 4 5 4 5 6
During execution in MATLAB command window, the matrix will be as shown below −
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> sa = a(2:3,2:4) sa = 3 4 5 4 5 6 >>