Types of Curves in Computer Graphics

---

---

Curves play an important role in computer graphics to create smooth and detailed shapes that line segments alone cannot achieve. Line segments are useful for representing straight-edged objects like triangles or squares, while curves are essential for more complex shapes such as circles or other smooth-edged forms.

In this chapter, we will see different types of curves used in computer graphics. We will cover implicit, explicit, parametric curves, and focus on important curve types like Bézier and B-spline curves.

Curves in Computer Graphics

A curve consists of an infinite set of points that are connected in a continuous manner. Each point on the curve typically has two neighbours, except for the endpoints. These endpoints, if they exist, have only one neighbour.

For example, in a circle, which is a closed curve, there are no endpoints because the curve forms a continuous loop. On the other hand, in an open curve like a line, the endpoints are the two points at the beginning and end of the curve.

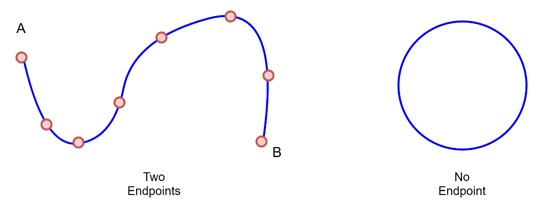
As we know, a curve consists of an infinitely large set of points. Any point on the curve has two neighbours except for a small number of points known as endpoints, which have only one neighbour.

Curves are useful for drawing objects that are not flat. Real-world objects often require curves to give them a more realistic and smooth appearance. Now, let us see some different types of curves commonly used in computer graphics.

Types of Curves

There are several ways to represent curves in computer graphics, and these are generally classified into three main categories:

• Implicit Curves
• Explicit Curves
• Parametric Curves
  • Bézier Curves
  • B-spline Curves

In the following sections of this chapter, we will elaborate these curves and their characteristic features.

Implicit Curves

From the name suggests, an implicit curve is defined by a mathematical function that checks whether a point lies on the curve or not.

The implicit function is often written as −

$$\mathrm{f(x,\: y) \:=\: 0}$$

In this case, the curve is formed by all the points (x, y) that satisfy the equation. Implicit curves are useful because they can describe a variety of complex shapes, but they have some limitations.

For example, the function cannot easily represent vertical lines or more complex curves without adding complexity to the mathematical expression.

Explicit Curves

In contrast, an explicit curve is represented as a function of one variable −

$$\mathrm{y \:=\: f(x)}$$

Here, for every value of x, there is a corresponding value of y. This representation works well for simple curves but cannot represent more complex shapes, especially those with vertical lines.

For example, the case of a circle or a complex curved object, explicit curves become limited since they are unable to represent vertical lines or more complicated shapes.

Parametric Curves

Parametric curves are the most used curves in modern computer graphics. These curves are defined using parametric equations, where each coordinate (x, y) of the curve is a function of one or more parameters, usually denoted by t. A common parametric curve is written as −

$$\mathrm{q(t) \:=\: (f(t),\: g(t))}$$

Where f(t) and g(t) are functions that define the x and y coordinates of the curve, respectively, and t is the parameter that varies over a certain range, usually between 0 and 1.

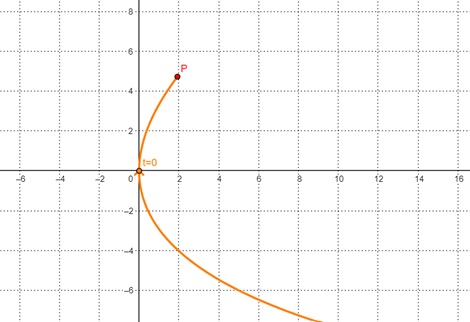
This is the example of a parametric curve for −

$$\mathrm{x(t) \:=\: 5t^2,\: \quad y(t) \:=\: t^2 \:+\: 7t}$$

Importance of Parametric Curves

Parametric curves allow for greater flexibility and control over the curve's shape. They are widely used in animation, modeling, and simulations. Most curves used today in 2D and 3D graphics are parametric because they allow for more precise control and smoothness.

Now that we understand the basic types of curves, let us dive deeper into two specific and widely used curves: Bézier curves and B-spline curves.

Bézier Curves

Bezier curves are used extensively in computer graphics, especially in vector graphics and animations. These curves are defined using control points, which determine the shape of the curve. A quadratic Bezier curve is defined as:

$$\mathrm{B(t) \:=\: (1 \:-\: t)^2 P_0 \:+\: 2(1 \:-\: t) t P_1 \:+\: t^2 P_2}$$

where P0, P1, and P2 are control points, and t is a parameter that varies between 0 and 1. Bezier curves allow designers to create smooth, flowing shapes and are widely used in drawing tools like Adobe Illustrator.

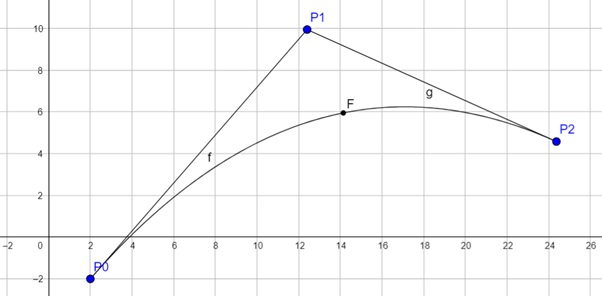
Application of Bézier Curves

Bézier curves are often used in 2D graphics applications such as illustration software and animation. They are used to create smooth curves in logos, animations, and other graphic designs.

However, one limitation of Bézier curves is that changing one of the control points can affect the entire shape of the curve, which can be undesirable in certain modelling scenarios.

B-spline Curves

The next famous type of curve is B-spline curves. B-splines offer better control over the shape of the curve by allowing local adjustments to the curve without affecting the entire shape. This makes them particularly useful in 3D modelling and computer-aided design (CAD) applications.

Unlike Bézier curves, where changing one control point affects the entire curve, B-spline curves allow for more localized changes. If a control point is moved in a B-spline curve, only a specific segment of the curve changes, leaving the rest of the curve intact.

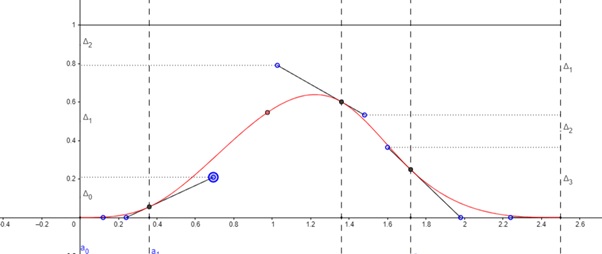
How Do B-spline Curves Work?

Like Bézier curves, B-splines are defined by control points. However, in a B-spline curve, the influence of each control point is limited to a local region of the curve. This allows designers to make more precise adjustments without altering the overall shape drastically.

Application of B-spline Curves

B-splines are widely used in where high-precision modelling is needed, such as automotive design, aerospace, and animation. They are also common in CAD software, where complex 3D shapes are needed.

Conclusion

In this chapter, we covered the different types of curves used in computer graphics. We understood the basic types, including implicit, explicit, and parametric curves. Then, we explored Bézier curves, which are widely used for 2D applications, and B-spline curves, which offer more flexibility and control, especially for 3D modeling. In the next a few chapters, we will cover the Bézier curves and B-Spline curves in detail.