- Surface Areas
- Home
- Nets of solids
- Surface area of a cube or a rectangular prism
- Surface area of a rectangular prism made of unit cubes
- Distinguishing between surface area and volume
- Using a net to find the surface area of a rectangular prism
- Word problem involving the surface area of a rectangular prism
- Surface area of a triangular prism
- Using a net to find the surface area of a triangular prism
Nets of solids
Introduction
A geometry net is a two-dimensional shape that can be folded to form a three-dimensional shape or a solid. When the surface of a three-dimensional figure is laid out flat showing each face of the figure, the pattern obtained is the net. Here are some steps we must take to determine whether a net forms a solid −
We ensure that the solid and the net have the same number of faces and that there is a match between the shapes of the faces of the solid and the shapes of the corresponding faces in the net.
We visualize how the net is to be folded to form the solid and ensure that all the sides fit together properly.
Nets are useful in finding the surface area of the solids.
Nets of Prisms, Pyramids, Cylinders and Cones
Here are some examples of nets of solids: Prism, Pyramid, Cylinder and Cone.
| Name | Shape | Net |
|---|---|---|
| Cube | 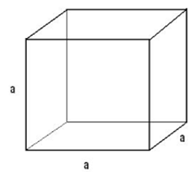 |
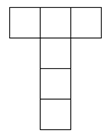 |
| Rectangular prism | 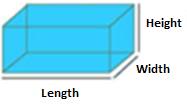 |
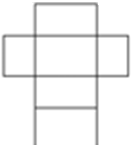 |
| Triangular prism | 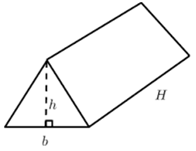 |
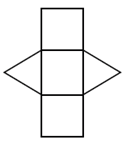 |
| Cylinder | 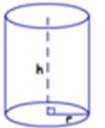 |
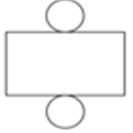 |
| Cone | 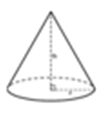 |
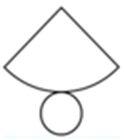 |
| Square pyramid | 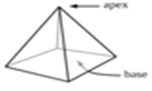 |
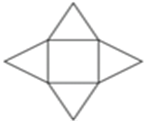 |
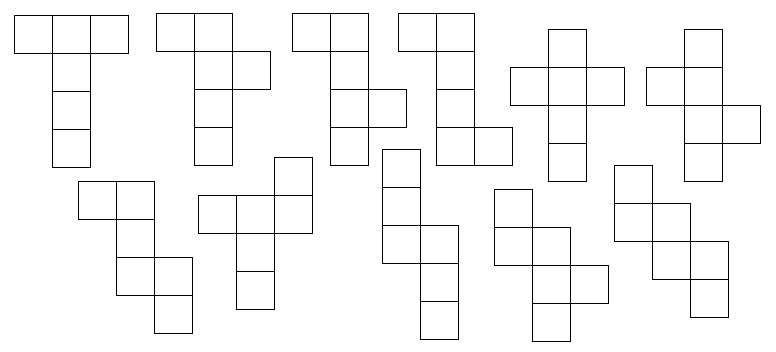
A solid may have different nets. There are altogether 11 possible nets for a cube as shown in the following figures.

Example 1
Sketch the net of the solid shape given below.

Solution
Step 1:
If the prism is unfolded along its edges we get the following net.
Step 2:
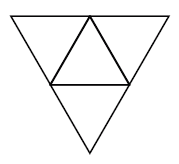
The net of a Triangular prism is as follows.

Example 2
Sketch the net of the solid shape given below.

Solution
Step 1:
If the pyramid is unfolded along its edges we get the following net.
Step 2:
The net of the Triangular pyramid is as follows.