Power Electronics - Performance Parameters

---

---

It is important to determine the performance parameters for different converters whose topologies can be single phase or multi-phase.

Assumptions

• The devices used are ideal, that is, they do not have any losses
• The devices have resistive loads

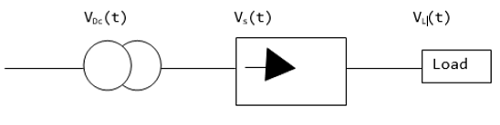
DC Voltage on Load

$$V_{DC}=\frac{1}{T} \int_{0}^{T}V_{L}\left ( t \right )dt$$

RMS Voltage on Load

$$V_{L}=\sqrt{\frac{1}{T}}\int_{0}^{T}V_{L}^{2}\left ( t \right )dt$$

Form Factor

$$FF=\frac{V_{L}}{V_{DC}}$$

Ripple Factor

$$RF=\frac{\sqrt{V_{L}^{2}-V_{DC}^{2}}}{V_{DC}}=\sqrt{FF^{2}-1}$$

Efficiency(Rectification Factor)

$$\eta =\frac{P_{DC}}{P_{L}+P_{D}}$$

Where the above are defined as −

$P_{DC}=V_{DC}\times I_{DC}$

$P_{L}=V_{L}\times I_{L}$

$P_{D}=R_{D}\times I_{L}^{2}$($P_{D}$ is the rectifier losses and $R_{D}$ the resistance)

$$\eta =\frac{V_{DC}I_{DC}}{\left ( V_{L}I_{L} \right )+\left ( R_{D}I_{L}^{2} \right )}=\frac{V_{DC}^{2}}{V_{L}^{2}}\times \frac{1}{1+\frac{R_{D}}{R_{L}}}$$

But $R_{D}=0$

Therefore,

$$\eta =\left ( \frac{V_{DC}}{V_{L}} \right )^{2}=\left ( \frac{1}{FF}\right )^{2}$$

Transformer Utilization Factor

$$TUF=\frac{P_{DC}}{VA \:Rating \:of \:the \:Transformer }=\frac{P_{DC}}{\frac{VA_{p}+VA_{s}}{2}}$$

VA_p and VA_s are the primary and secondary power ratings of the transformer.