
- Graph Theory - Home
- Graph Theory - Introduction
- Graph Theory - History
- Graph Theory - Fundamentals
- Graph Theory - Applications
- Types of Graphs
- Graph Theory - Types of Graphs
- Graph Theory - Simple Graphs
- Graph Theory - Multi-graphs
- Graph Theory - Directed Graphs
- Graph Theory - Weighted Graphs
- Graph Theory - Bipartite Graphs
- Graph Theory - Complete Graphs
- Graph Theory - Subgraphs
- Graph Theory - Trees
- Graph Theory - Forests
- Graph Theory - Planar Graphs
- Graph Theory - Hypergraphs
- Graph Theory - Infinite Graphs
- Graph Theory - Random Graphs
- Graph Representation
- Graph Theory - Graph Representation
- Graph Theory - Adjacency Matrix
- Graph Theory - Adjacency List
- Graph Theory - Incidence Matrix
- Graph Theory - Edge List
- Graph Theory - Compact Representation
- Graph Theory - Incidence Structure
- Graph Theory - Matrix-Tree Theorem
- Graph Properties
- Graph Theory - Basic Properties
- Graph Theory - Coverings
- Graph Theory - Matchings
- Graph Theory - Independent Sets
- Graph Theory - Traversability
- Graph Theory Connectivity
- Graph Theory - Connectivity
- Graph Theory - Vertex Connectivity
- Graph Theory - Edge Connectivity
- Graph Theory - k-Connected Graphs
- Graph Theory - 2-Vertex-Connected Graphs
- Graph Theory - 2-Edge-Connected Graphs
- Graph Theory - Strongly Connected Graphs
- Graph Theory - Weakly Connected Graphs
- Graph Theory - Connectivity in Planar Graphs
- Graph Theory - Connectivity in Dynamic Graphs
- Special Graphs
- Graph Theory - Regular Graphs
- Graph Theory - Complete Bipartite Graphs
- Graph Theory - Chordal Graphs
- Graph Theory - Line Graphs
- Graph Theory - Complement Graphs
- Graph Theory - Graph Products
- Graph Theory - Petersen Graph
- Graph Theory - Cayley Graphs
- Graph Theory - De Bruijn Graphs
- Graph Algorithms
- Graph Theory - Graph Algorithms
- Graph Theory - Breadth-First Search
- Graph Theory - Depth-First Search (DFS)
- Graph Theory - Dijkstra's Algorithm
- Graph Theory - Bellman-Ford Algorithm
- Graph Theory - Floyd-Warshall Algorithm
- Graph Theory - Johnson's Algorithm
- Graph Theory - A* Search Algorithm
- Graph Theory - Kruskal's Algorithm
- Graph Theory - Prim's Algorithm
- Graph Theory - Borůvka's Algorithm
- Graph Theory - Ford-Fulkerson Algorithm
- Graph Theory - Edmonds-Karp Algorithm
- Graph Theory - Push-Relabel Algorithm
- Graph Theory - Dinic's Algorithm
- Graph Theory - Hopcroft-Karp Algorithm
- Graph Theory - Tarjan's Algorithm
- Graph Theory - Kosaraju's Algorithm
- Graph Theory - Karger's Algorithm
- Graph Coloring
- Graph Theory - Coloring
- Graph Theory - Edge Coloring
- Graph Theory - Total Coloring
- Graph Theory - Greedy Coloring
- Graph Theory - Four Color Theorem
- Graph Theory - Coloring Bipartite Graphs
- Graph Theory - List Coloring
- Advanced Topics of Graph Theory
- Graph Theory - Chromatic Number
- Graph Theory - Chromatic Polynomial
- Graph Theory - Graph Labeling
- Graph Theory - Planarity & Kuratowski's Theorem
- Graph Theory - Planarity Testing Algorithms
- Graph Theory - Graph Embedding
- Graph Theory - Graph Minors
- Graph Theory - Isomorphism
- Spectral Graph Theory
- Graph Theory - Graph Laplacians
- Graph Theory - Cheeger's Inequality
- Graph Theory - Graph Clustering
- Graph Theory - Graph Partitioning
- Graph Theory - Tree Decomposition
- Graph Theory - Treewidth
- Graph Theory - Branchwidth
- Graph Theory - Graph Drawings
- Graph Theory - Force-Directed Methods
- Graph Theory - Layered Graph Drawing
- Graph Theory - Orthogonal Graph Drawing
- Graph Theory - Examples
- Computational Complexity of Graph
- Graph Theory - Time Complexity
- Graph Theory - Space Complexity
- Graph Theory - NP-Complete Problems
- Graph Theory - Approximation Algorithms
- Graph Theory - Parallel & Distributed Algorithms
- Graph Theory - Algorithm Optimization
- Graphs in Computer Science
- Graph Theory - Data Structures for Graphs
- Graph Theory - Graph Implementations
- Graph Theory - Graph Databases
- Graph Theory - Query Languages
- Graph Algorithms in Machine Learning
- Graph Neural Networks
- Graph Theory - Link Prediction
- Graph-Based Clustering
- Graph Theory - PageRank Algorithm
- Graph Theory - HITS Algorithm
- Graph Theory - Social Network Analysis
- Graph Theory - Centrality Measures
- Graph Theory - Community Detection
- Graph Theory - Influence Maximization
- Graph Theory - Graph Compression
- Graph Theory Real-World Applications
- Graph Theory - Network Routing
- Graph Theory - Traffic Flow
- Graph Theory - Web Crawling Data Structures
- Graph Theory - Computer Vision
- Graph Theory - Recommendation Systems
- Graph Theory - Biological Networks
- Graph Theory - Social Networks
- Graph Theory - Smart Grids
- Graph Theory - Telecommunications
- Graph Theory - Knowledge Graphs
- Graph Theory - Game Theory
- Graph Theory - Urban Planning
- Graph Theory Useful Resources
- Graph Theory - Quick Guide
- Graph Theory - Useful Resources
- Graph Theory - Discussion
Graph Theory - Types of Graphs
There are various types of graphs depending upon the number of vertices, number of edges, interconnectivity, and their overall structure. We will discuss only a certain few important types of graphs in this chapter.
Null Graph
A graph having no edges is called a Null Graph.
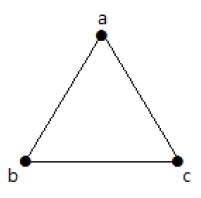
Example

In the above graph, there are three vertices named a, b, and c, but there are no edges among them. Hence it is a Null Graph.
Trivial Graph
A graph with only one vertex is called a Trivial Graph.
Example

In the above shown graph, there is only one vertex a with no other edges. Hence it is a Trivial graph.
Non-Directed Graph
A non-directed graph contains edges but the edges are not directed ones.
Example

In this graph, a, b, c, d, e, f, g are the vertices, and ab, bc, cd, da, ag, gf, ef are the edges of the graph. Since it is a non-directed graph, the edges ab and ba are same. Similarly other edges also considered in the same way.
Directed Graph
In a directed graph, each edge has a direction.
Example
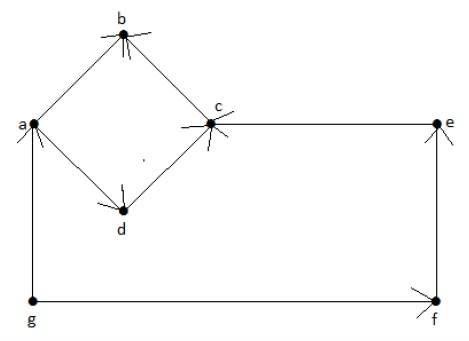
In the above graph, we have seven vertices a, b, c, d, e, f, and g, and eight edges ab, cb, dc, ad, ec, fe, gf, and ga. As it is a directed graph, each edge bears an arrow mark that shows its direction. Note that in a directed graph, ab is different from ba.
Simple Graph
A graph with no loops and no parallel edges is called a simple graph.
The maximum number of edges possible in a single graph with n vertices is nC2 where nC2 = n(n 1)/2.
The number of simple graphs possible with n vertices = 2nc2 = 2n(n-1)/2.
Example
In the following graph, there are 3 vertices with 3 edges which is maximum excluding the parallel edges and loops. This can be proved by using the above formulae.
The maximum number of edges with n=3 vertices −
nC2 = n(n1)/2 = 3(31)/2 = 6/2 = 3 edges
The maximum number of simple graphs with n=3 vertices −
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
These 8 graphs are as shown below −

Connected Graph
A graph G is said to be connected if there exists a path between every pair of vertices. There should be at least one edge for every vertex in the graph. So that we can say that it is connected to some other vertex at the other side of the edge.
Example
In the following graph, each vertex has its own edge connected to other edge. Hence it is a connected graph.
Disconnected Graph
A graph G is disconnected, if it does not contain at least two connected vertices.
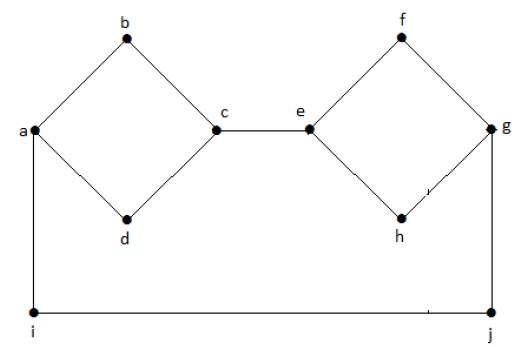
Example 1
The following graph is an example of a Disconnected Graph, where there are two components, one with a, b, c, d vertices and another with e, f, g, h vertices.
The two components are independent and not connected to each other. Hence it is called disconnected graph.
Example 2

In this example, there are two independent components, a-b-f-e and c-d, which are not connected to each other. Hence this is a disconnected graph.
Regular Graph
A graph G is said to be regular, if all its vertices have the same degree. In a graph, if the degree of each vertex is k, then the graph is called a k-regular graph.
Example
In the following graphs, all the vertices have the same degree. So these graphs are called regular graphs.
In both the graphs, all the vertices have degree 2. They are called 2-Regular Graphs.
Complete Graph
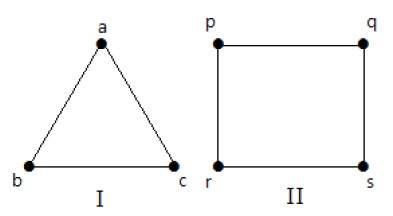
A simple graph with n mutual vertices is called a complete graph and it is denoted by Kn. In the graph, a vertex should have edges with all other vertices, then it called a complete graph.
In other words, if a vertex is connected to all other vertices in a graph, then it is called a complete graph.
Example
In the following graphs, each vertex in the graph is connected with all the remaining vertices in the graph except by itself.
In graph I,
| a | b | c | |
|---|---|---|---|
| a | Not Connected | Connected | Connected |
| b | Connected | Not Connected | Connected |
| c | Connected | Connected | Not Connected |
In graph II,
| p | q | r | s | |
|---|---|---|---|---|
| p | Not Connected | Connected | Connected | Connected |
| q | Connected | Not Connected | Connected | Connected |
| r | Connected | Connected | Not Connected | Connected |
| s | Connected | Connected | Connected | Not Connected |
Cycle Graph
A simple graph with n vertices (n >= 3) and n edges is called a cycle graph if all its edges form a cycle of length n.
If the degree of each vertex in the graph is two, then it is called a Cycle Graph.
Notation − Cn
Example
Take a look at the following graphs −
Graph I has 3 vertices with 3 edges which is forming a cycle ab-bc-ca.
Graph II has 4 vertices with 4 edges which is forming a cycle pq-qs-sr-rp.
Graph III has 5 vertices with 5 edges which is forming a cycle ik-km-ml-lj-ji.
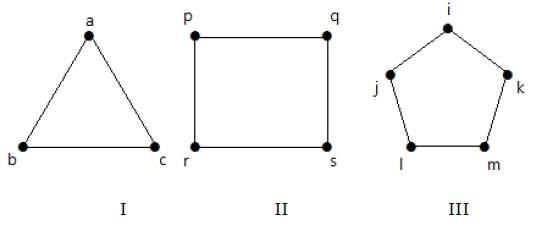
Hence all the given graphs are cycle graphs.
Wheel Graph
A wheel graph is obtained from a cycle graph Cn-1 by adding a new vertex. That new vertex is called a Hub which is connected to all the vertices of Cn.
Notation − Wn
No. of edges in Wn = No. of edges from hub to all other vertices +
No. of edges from all other nodes in cycle graph without a hub.
= (n1) + (n1)
= 2(n1)
Example
Take a look at the following graphs. They are all wheel graphs.
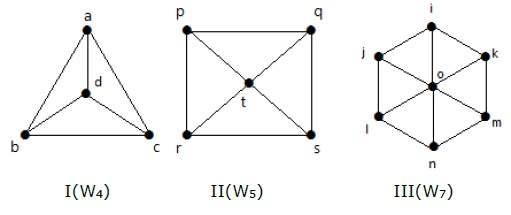
In graph I, it is obtained from C3 by adding an vertex at the middle named as d. It is denoted as W4.
Number of edges in W4 = 2(n-1) = 2(3) = 6
In graph II, it is obtained from C4 by adding a vertex at the middle named as t. It is denoted as W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
In graph III, it is obtained from C6 by adding a vertex at the middle named as o. It is denoted as W7.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Cyclic Graph
A graph with at least one cycle is called a cyclic graph.
Example
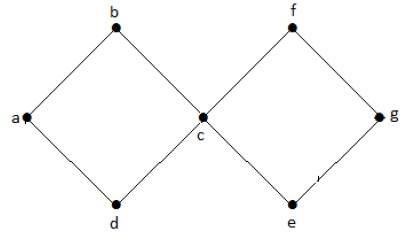
In the above example graph, we have two cycles a-b-c-d-a and c-f-g-e-c. Hence it is called a cyclic graph.
Acyclic Graph
A graph with no cycles is called an acyclic graph.
Example
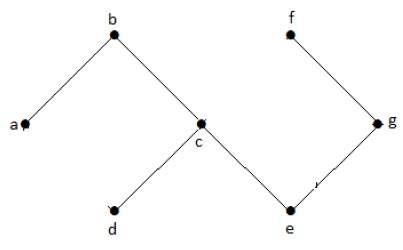
In the above example graph, we do not have any cycles. Hence it is a non-cyclic graph.
Bipartite Graph
A simple graph G = (V, E) with vertex partition V = {V1, V2} is called a bipartite graph if every edge of E joins a vertex in V1 to a vertex in V2.
In general, a Bipertite graph has two sets of vertices, let us say, V1 and V2, and if an edge is drawn, it should connect any vertex in set V1 to any vertex in set V2.
Example
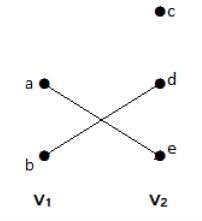
In this graph, you can observe two sets of vertices − V1 and V2. Here, two edges named ae and bd are connecting the vertices of two sets V1 and V2.
Complete Bipartite Graph
A bipartite graph G, G = (V, E) with partition V = {V1, V2} is said to be a complete bipartite graph if every vertex in V1 is connected to every vertex of V2.
In general, a complete bipartite graph connects each vertex from set V1 to each vertex from set V2.
Example
The following graph is a complete bipartite graph because it has edges connecting each vertex from set V1 to each vertex from set V2.
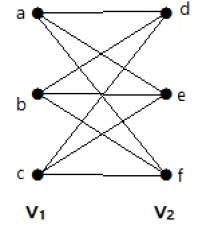
If |V1| = m and |V2| = n, then the complete bipartite graph is denoted by Km, n.
Km,n has (m+n) vertices and (mn) edges.
Km,n is a regular graph if m=n.
In general, a complete bipartite graph is not a complete graph.
Km,n is a complete graph if m=n=1.
The maximum number of edges in a bipartite graph with n vertices is
If n=10, k5, 5= ⌊ n2 4 ⌋ = ⌊ 102 4 ⌋ = 25
Similarly K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
If n=9, k5, 4 = ⌊ n2 4 ⌋ = ⌊ 92 4 ⌋ = 20
Similarly K6, 3=18
K7, 2=14
K8, 1=8
G is a bipartite graph if G has no cycles of odd length. A special case of bipartite graph is a star graph.
Star Graph
A complete bipartite graph of the form K1, n-1 is a star graph with n-vertices. A star graph is a complete bipartite graph if a single vertex belongs to one set and all the remaining vertices belong to the other set.
Example
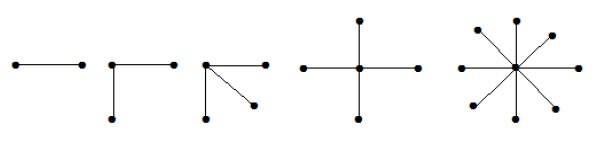
In the above graphs, out of n vertices, all the n1 vertices are connected to a single vertex. Hence it is in the form of K1, n-1 which are star graphs.
Complement of a Graph
Let 'G−' be a simple graph with some vertices as that of G and an edge {U, V} is present in 'G−', if the edge is not present in G. It means, two vertices are adjacent in 'G−' if the two vertices are not adjacent in G.
If the edges that exist in graph I are absent in another graph II, and if both graph I and graph II are combined together to form a complete graph, then graph I and graph II are called complements of each other.
Example
In the following example, graph-I has two edges cd and bd. Its complement graph-II has four edges.

Note that the edges in graph-I are not present in graph-II and vice versa. Hence, the combination of both the graphs gives a complete graph of n vertices.
Note − A combination of two complementary graphs gives a complete graph.
If G is any simple graph, then
|E(G)| + |E('G-')| = |E(Kn)|, where n = number of vertices in the graph.
Example
Let G be a simple graph with nine vertices and twelve edges, find the number of edges in 'G-'.
You have, |E(G)| + |E('G-')| = |E(Kn)|
12 + |E('G-')| =
9(9-1) 2 = 9C212 + |E('G-')| = 36
|E('G-')| = 24
G is a simple graph with 40 edges and its complement 'G−' has 38 edges. Find the number of vertices in the graph G or 'G−'.
Let the number of vertices in the graph be n.
We have, |E(G)| + |E('G-')| = |E(Kn)|
40 + 38 = n(n-1) 2
156 = n(n-1)
13(12) = n(n-1)
n = 13