
- Excel Functions - Home
- Compatibility Functions
- Compatibility Functions
- BETADIST Function
- BETAINV Function
- BINOMDIST Function
- CEILING Function
- CHIDIST Function
- CHIINV Function
- CHITEST Function
- CONFIDENCE Function
- COVAR Function
- CRITBINOM Function
- EXPONDIST Function
- FDIST Function
- FINV Function
- FLOOR Function
- FTEST Function
- GAMMADIST Function
- GAMMAINV Function
- HYPGEOMDIST Function
- LOGINV Function
- LOGNORMDIST Function
- MODE Function
- NEGBINOMDIST Function
- NORMDIST Function
- NORMINV Function
- NORMSDIST Function
- NORMSINV Function
- PERCENTILE Function
- PERCENTRANK Function
- POISSON Function
- QUARTILE Function
- RANK Function
- STDEV Function
- STDEVP Function
- TDIST Function
- TINV Function
- TTEST Function
- VAR Function
- VARP Function
- WEIBULL Function
- ZTEST Function
- Logical Functions
- Logical Functions
- AND Function
- FALSE Function
- IF Function
- IFERROR Function
- IFNA Function
- IFS Function
- NOT Function
- OR Function
- SWITCH Function
- TRUE Function
- XOR Function
- Text Functions
- Text Functions
- ARRAYTOTEXT Function
- BAHTTEXT Function
- CHAR Function
- CLEAN Function
- CODE Function
- CONCAT Function
- CONCATENATE Function
- DBCS Function
- DOLLAR Function
- Exact Function
- FIND Function
- FINDB Function
- FIXED Function
- LEFT Function
- LEFTB Function
- LEN Function
- LENB Function
- LOWER Function
- MID Function
- MIDB Function
- NUMBERVALUE Function
- PHONETIC Function
- PROPER Function
- REPLACE Function
- REPLACEB Function
- REPT Function
- RIGHT Function
- RIGHTB Function
- SEARCH Function
- SEARCHB Function
- SUBSTITUTE Function
- T Function
- TEXT Function
- TEXTAFTER Function
- TEXTBEFORE Function
- TEXTJOIN Function
- TEXTSPLIT Function
- TRIM Function
- UNICHAR Function
- UNICODE Function
- UPPER Function
- VALUE Function
- VALUETOTEXT Function
- Date & Time Functions
- Date & Time Functions
- DATE Function
- DATEDIF Function
- DATEVALUE Function
- DAY Function
- DAYS Function
- DAYS360 Function
- EDATE Function
- EOMONTH Function
- HOUR Function
- ISOWEEKNUM Function
- MINUTE Function
- MONTH Function
- NETWORKDAYS Function
- NETWORKDAYS.INTL Function
- NOW Function
- SECOND Function
- TIME Function
- TIMEVALUE Function
- TODAY Function
- WEEKDAY Function
- WEEKNUM Function
- WORKDAY Function
- WORKDAY.INTL Function
- YEAR Function
- YEARFRAC Function
- Cube Functions
- Cube Functions
- CUBEKPIMEMBER Function
- CUBEMEMBER Function
- CUBEMEMBERPROPERTY Function
- CUBERANKEDMEMBER Function
- CUBESET Function
- CUBESETCOUNT Function
- CUBEVALUE Function
- Math Functions
- Math Functions
- ABS Function
- AGGREGATE Function
- ARABIC Function
- BASE Function
- CEILING.MATH Function
- COMBIN Function
- COMBINA Function
- DECIMAL Function
- DEGREES Function
- EVEN Function
- EXP Function
- FACT Function
- FACTDOUBLE Function
- FLOOR.MATH Function
- GCD Function
- INT Function
- LCM Function
- LN Function
- LOG Function
- LOG10 Function
- MDETERM Function
- MINVERSE Function
- MMULT Function
- MOD Function
- MROUND Function
- MULTINOMIAL Function
- MUNIT Function
- ODD Function
- PI Function
- POWER Function
- PRODUCT Function
- QUOTIENT Function
- RADIANS Function
- RAND Function
- RANDBETWEEN Function
- ROMAN Function
- ROUND Function
- ROUNDDOWN Function
- ROUNDUP Function
- SERIESSUM Function
- SIGN Function
- SQRT Function
- SQRTPI Function
- SUBTOTAL Function
- SUM Function
- SUMIF Function
- SUMIFS Function
- SUMPRODUCT Function
- SUMSQ Function
- SUMX2MY2 Function
- SUMX2PY2 Function
- SUMXMY2 Function
- TRUNC Function
- Trigonometric Functions
- Trigonometric Functions
- ACOS
- ACOSH Function
- ACOT Function
- ACOTH Function
- ASIN Function
- ASINH Function
- ATAN Function
- ATAN2 Function
- ATANH Function
- COS Function
- COSH Function
- COT Function
- COTH Function
- CSC Function
- CSCH Function
- SEC Function
- SECH Function
- SIN Function
- SINH Function
- TAN Function
- TANH Function
- Database Functions
- Database Functions
- DAVERAGE
- DCOUNT
- DCOUNTA
- DGET
- DMAX
- DMIN
- DPRODUCT
- DSTDEV
- DSTDEVP
- DSUM
- DVAR
- DVARP
- Dynamic Array Functions
- Dynamic Array Functions
- FILTER Function
- RANDARRAY Function
- SEQUENCE Function
- SORT Function
- SORTBY Function
- UNIQUE Function
- XLOOKUP Function
- XMATCH Function
- Engineering Functions
- Engineering Functions
- BESSELI Function
- BESSELJ Function
- BESSELK Function
- BESSELY Function
- BIN2DEC Function
- BIN2HEX Function
- BIN2OCT Function
- BITAND Function
- BITLSHIFT Function
- BITOR Function
- BITRSHIFT Function
- BITXOR Function
- COMPLEX Function
- CONVERT Function
- DEC2BIN Function
- DEC2HEX Function
- DEC2OCT Function
- DELTA Function
- ERF Function
- ERF.PRECISE Function
- ERFC Function
- ERFC.PRECISE Function
- GESTEP Function
- HEX2BIN Function
- HEX2DEC Function
- HEX2OCT Function
- IMABS Function
- IMAGINARY Function
- IMARGUMENT Function
- IMCONJUGATE Function
- IMCOS Function
- IMCOSH Function
- IMCOT Function
- IMCSC Function
- IMCSCH Function
- IMDIV Function
- IMEXP Function
- IMLN Function
- IMLOG2 Function
- IMLOG10 Function
- IMPOWER Function
- IMPRODUCT Function
- IMREAL Function
- IMSEC Function
- IMSECH Function
- IMSIN Function
- IMSINH Function
- IMSQRT Function
- IMSUB Function
- IMSUM Function
- IMTAN Function
- OCT2BIN Function
- OCT2DEC Function
- OCT2HEX Function
- Financial Functions
- Financial Functions
- ACCRINT Function
- ACCRINTM Function
- AMORDEGRC Function
- AMORLINC Function
- COUPDAYBS Function
- COUPDAYS Function
- COUPDAYSNC Function
- COUPNCD Function
- COUPNUM Function
- COUPPCD Function
- CUMIPMT Function
- CUMPRINC Function
- DB Function
- DDB Function
- DISC Function
- DOLLARDE Function
- DOLLARFR Function
- DURATION Function
- EFFECT Function
- FV Function
- FVSCHEDULE Function
- INTRATE Function
- IPMT Function
- IRR Function
- ISPMT Function
- MDURATION Function
- MIRR Function
- NOMINAL Function
- NPER Function
- NPV Function
- ODDFPRICE Function
- ODDFYIELD Function
- ODDLPRICE Function
- ODDLYIELD Function
- PDURATION Function
- PMT Function
- PPMT Function
- PRICE Function
- PRICEDISC Function
- PRICEMAT Function
- PV Function
- RATE Function
- RECEIVED Function
- RRI Function
- SLN Function
- SYD Function
- TBILLEQ Function
- TBILLPRICE Function
- TBILLYIELD Function
- VDB Function
- XIRR Function
- XNPV Function
- YIELD Function
- YIELDDISC Function
- YIELDMAT Function
- Information Functions
- Information Functions
- CELL Function
- ERROR.TYPE Function
- INFO Function
- ISBLANK Function
- ISERR Function
- ISERROR Function
- ISEVEN Function
- ISFORMULA Function
- ISLOGICAL Function
- ISNA Function
- ISNONTEXT Function
- ISNUMBER Function
- ISODD Function
- ISREF Function
- ISTEXT Function
- N Function
- NA Function
- SHEET Function
- SHEETS Function
- TYPE Function
- Lookup & Reference Functions
- Lookup & Reference Functions
- ADDRESS Function
- AREAS Function
- CHOOSE Function
- COLUMN Function
- COLUMNS Function
- FORMULATEXT Function
- GETPIVOTDATA Function
- HLOOKUP Function
- HYPERLINK Function
- INDEX Function
- INDIRECT Function
- LOOKUP Function
- MATCH Function
- OFFSET Function
- ROW Function
- ROWS Function
- RTD Function
- TRANSPOSE Function
- VLOOKUP Function
- Statistical Functions
- Statistical Functions
- AVEDEV Function
- AVERAGE Function
- AVERAGEA Function
- AVERAGEIF Function
- AVERAGEIFS Function
- BETA.DIST Function
- BETA.INV Function
- BINOM.DIST Function
- BINOM.DIST.RANGE Function
- BINOM.INV Function
- CHISQ.DIST Function
- CHISQ.DIST.RT Function
- CHISQ.INV Function
- CHISQ.INV.RT Function
- CHISQ.TEST Function
- CONFIDENCE.NORM Function
- CONFIDENCE.T Function
- CORREL Function
- COUNT Function
- COUNTA Function
- COUNTBLANK Function
- COUNTIF Function
- COUNTIFS Function
- COVARIANCE.P Function
- COVARIANCE.S Function
- DEVSQ Function
- EXPON.DIST Function
- F.DIST Function
- F.DIST.RT Function
- F.INV Function
- F.INV.RT Function
- F.TEST Function
- FISHER Function
- FISHERINV Function
- FORECAST Function
- FORECAST.ETS Function
- FORECAST.ETS.CONFINT Function
- FORECAST.ETS.SEASONALITY Function
- FORECAST.ETS.STAT Function
- FORECAST.LINEAR Function
- FREQUENCY Function
- GAMMA Function
- GAMMA.DIST Function
- GAMMA.INV Function
- GAMMALN Function
- GAMMALN.PRECISE Function
- GAUSS Function
- GEOMEAN
- GROWTH
- HARMEAN
- HYPGEOM.DIST
- INTERCEPT Function
- KURT Function
- LARGE Function
- LINEST Function
- LOGEST Function
- LOGNORM.DIST Function
- LOGNORM.INV Function
- MAX Function
- MAXA Function
- MAXIFS Function
- MEDIAN Function
- MIN Function
- MINA Function
- MINIFS Function
- MODE.MULT Function
- MODE.SNGL Function
- NEGBINOM.DIST Function
- NORM.DIST Function
- NORM.INV Function
- NORM.S.DIST Function
- NORM.S.INV Function
- PEARSON Function
- PERCENTILE.EXC
- PERCENTILE.INC
- PERCENTRANK.EXC
- PERCENTRANK.INC
- PERMUT
- PERMUTATIONA
- PHI
- POISSON.DIST
- PROB
- QUARTILE.EXC
- QUARTILE.INC
- RANK.AVG
- RANK.EQ
- RSQ
- SKEW
- SKEW.P
- SLOPE
- SMALL
- STANDARDIZE
- STDEV.P
- STDEV.S
- STDEVA
- STDEVPA
- STEYX
- T.DIST
- T.DIST.2T
- T.DIST.RT
- T.INV
- T.INV.2T
- T.TEST
- TREND
- TRIMMEAN Function
- VAR.P Function
- VAR.S Function
- VARA Function
- VARPA Function
- WEIBULL.DIST Function
- Z.TEST Function
- Web Functions
- Web Functions
- ENCODEURL Function
- FILTERXML Function
- WEBSERVICE Function
Excel - GAMMAINV Function
GAMMAINV Function
The Excel GAMMAINV function retrieves the gamma cumulative distributions inverse. This function is employed in various fields, including medical, logistics, risk, and quality control management. For instance, it is used to determine the recovery time of hypertension patients from heart-related diseases.
The mathematical notation is t = GAMMADIST(x, ...) then GAMMAINV(t, ...) = x
The GAMMAINV function interchanges the GAMMA.INV function appended in Excel 2010.
Note − This function has been interchanged with new powerful functions with excellent accuracy. However, this function is still exclusive to backward compatibility.
Syntax
The syntax of GAMMAINV function is as follows −
GAMMAINV (probability,alpha,beta)
Compatibility
This advanced Excel function is compatible with the following versions of MS-Excel −
- Excel for Microsoft 365
- Excel for Microsoft 365 for Mac
- Excel for the Web
- Excel 2021
- Excel 2021 for Mac
- Excel 2019
- Excel 2019 for Mac
- Excel 2016
Arguments
You can use the following arguments with the GAMMAINV function −
| Argument | Description | Required / Optional |
|---|---|---|
| Probability | It specifies the probability linked with the gamma distribution. | Required |
| Alpha | It specifies the gamma distributions shape parameter | Required |
| Beta | It represents the gamma distributions scale parameter. | Required |
Points to Remember
- The GAMMAINV function retrieves the #VALUE! error if any of its arguments contains the text string.
- Either the probability is negative or greater than 1, GAMMAINV will receive the #NUM! Error.
- Either the Alpha or Beta value is less than or equal to zero, GAMMAINV returns the #NUM! Error.
- This function employs the iterative search technique. Suppose the search is unsuccessful after 100 iterations; the GAMMAINV function will retrieve the #N/A error.
- GAMMAINV function will retrieve the standard gamma distribution if the value of the Beta is equal to 1.
Examples of GAMMAINV Function
Practice the following examples to learn the use of the GAMMAINV function in Excel.
Example 1
Suppose the sales manager wishes to compute the time to failure of the electronic item Air fryer through the GAMMAINV function.
Solution
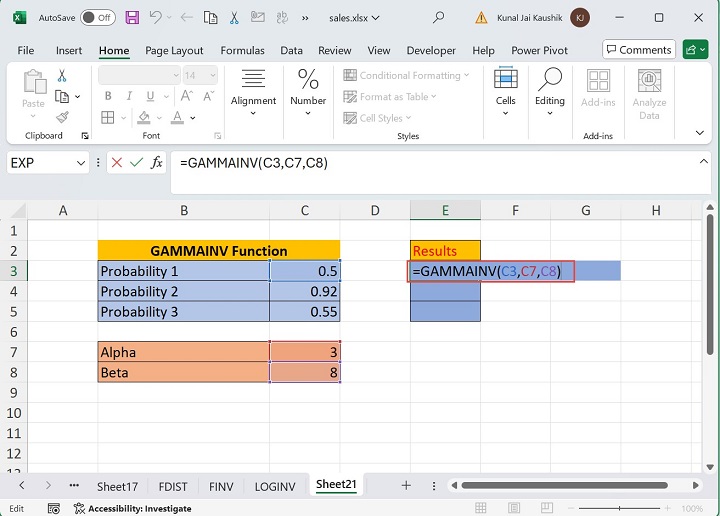
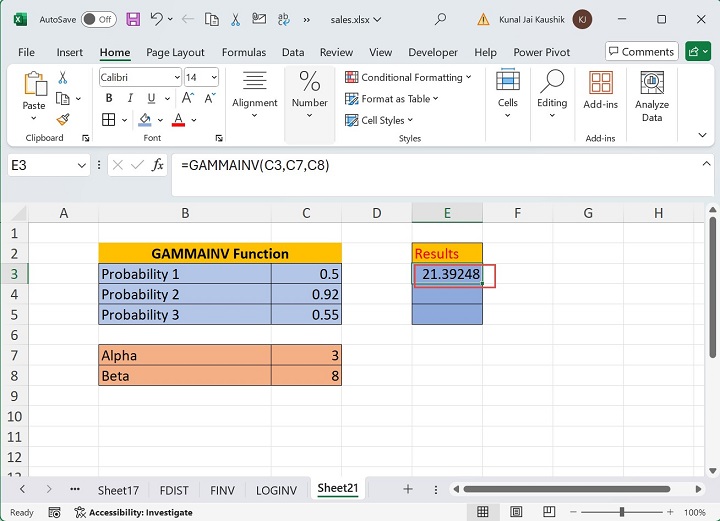
Assume the sample dataset, where the distinct probability values are defined in the range C3:C5. Calculate the GAMMAINV function for each given probability to evaluate the time to failure. Enter the formula =GAMMAINV(C3,C7,C8) in the E3 cell and press the Enter tab to get the result.
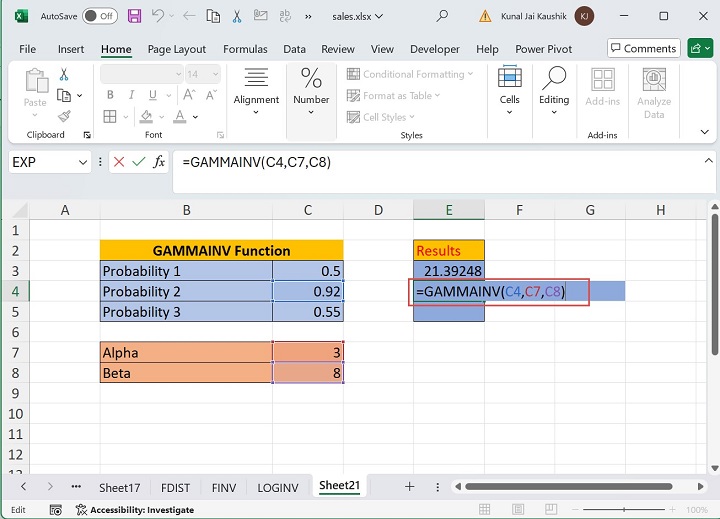
Similarly, enter the formula =GAMMAINV(C4,C7,C8) in the E4 cell and press the Enter tab.
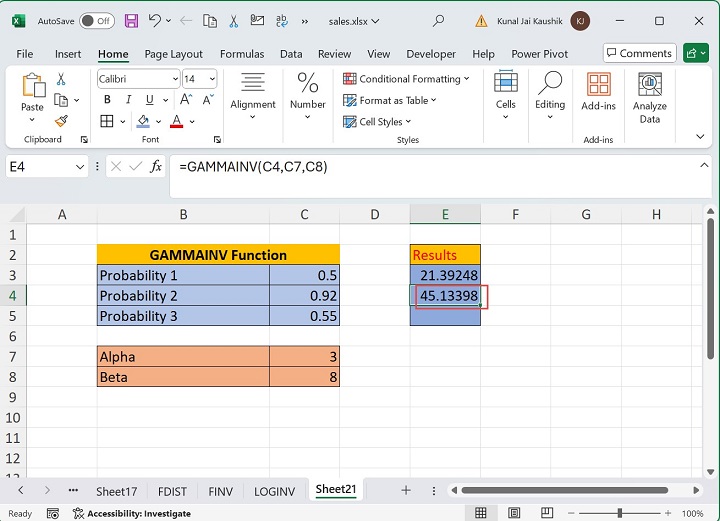
Therefore, the resultant value is 45.133 at the specified probability of 0.92, representing the time to failure.
Now, calculate the GAMMAINV function at the specified probability of 0.55, and enter the formula =GAMMAINV(C5,C7, C8) in the E5 cell.

And then press the Enter tab to get the resulting value.

Example 2
The GAMMAINV function retrieves the #VALUE! error if any of its arguments contains the text string.
Solution
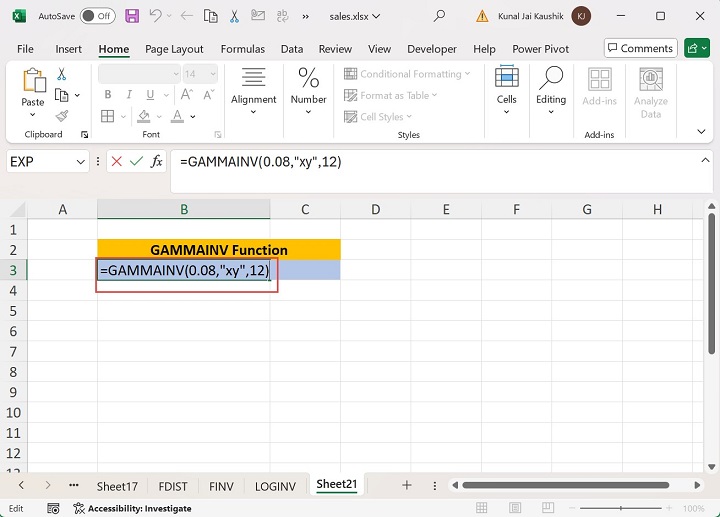
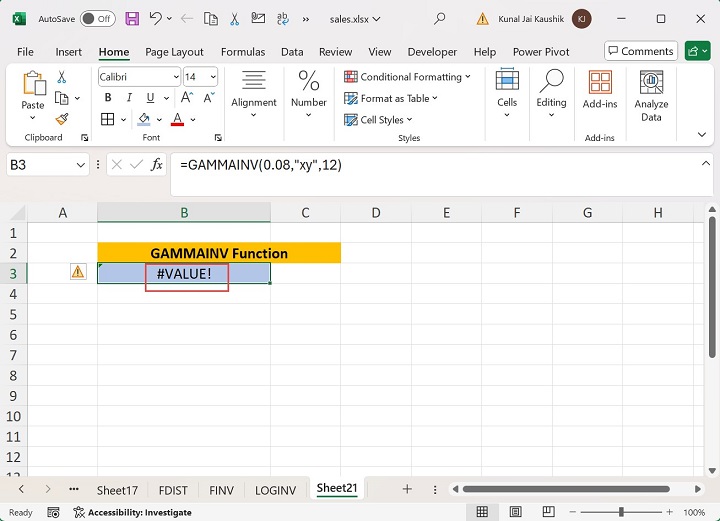
Example 3
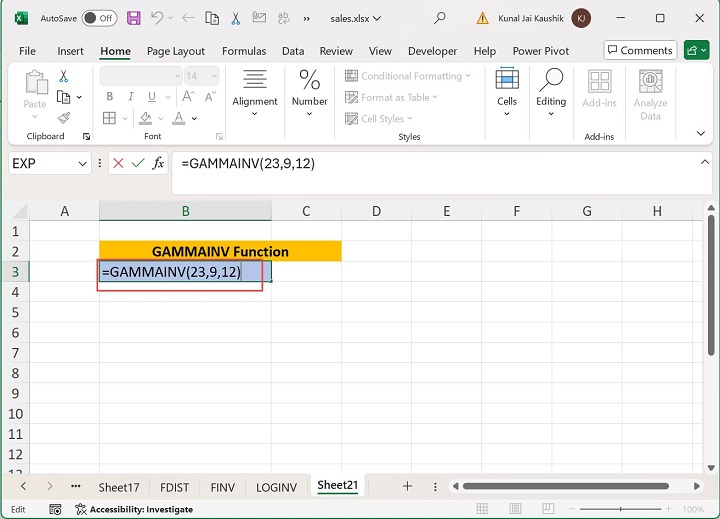
Either the probability is negative or greater than 1, the GAMMAINV function will receive the #NUM! Error.
Solution
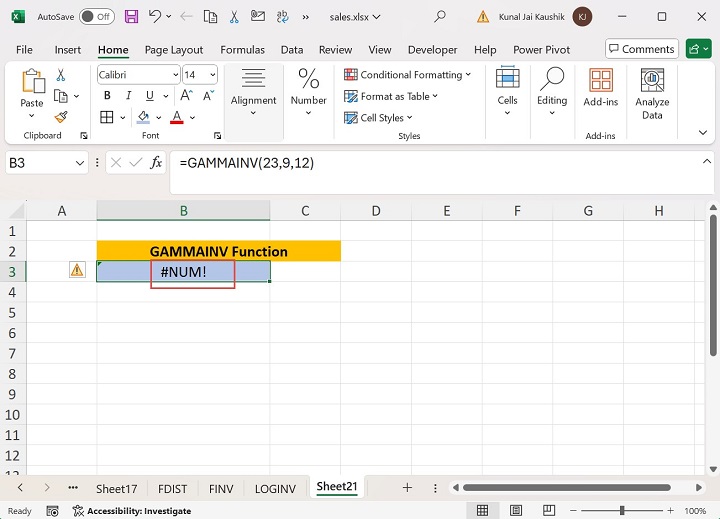
Write the formula =GAMMAINV(23,9,12) in the B3 cell. Here, the probability value is 23, greater than 1.
Therefore, the #NUM! error will occur.
Example 4
Either the Alpha or Beta value is less than and equal to zero, GAMMAINV returns the #NUM! Error.
Solution
If the value of Alpha is negative −
Enter the formula =GAMMAINV(0.34,-4,12) in the B3 cell and press the Enter tab. The #NUM! will then be obtained after executing this function.


If the value of Beta is 0 −
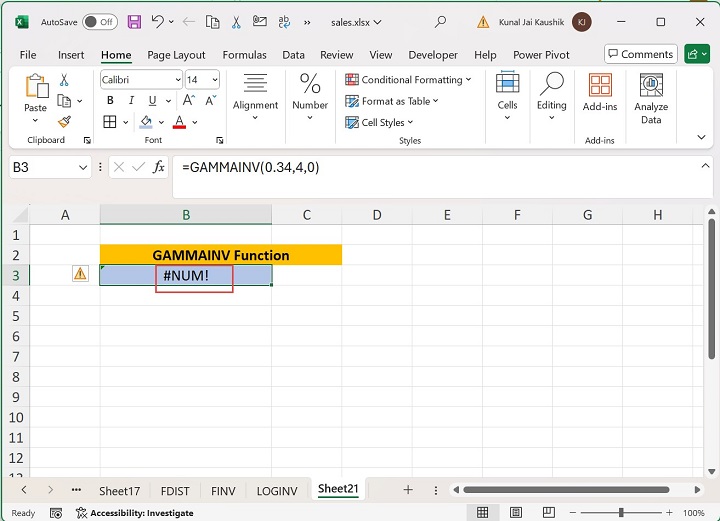
As you can notice in the screenshot, the third argument, Beta is 0. Enter the formula =GAMMAINV(0.34,4,0) in the B3 cell.
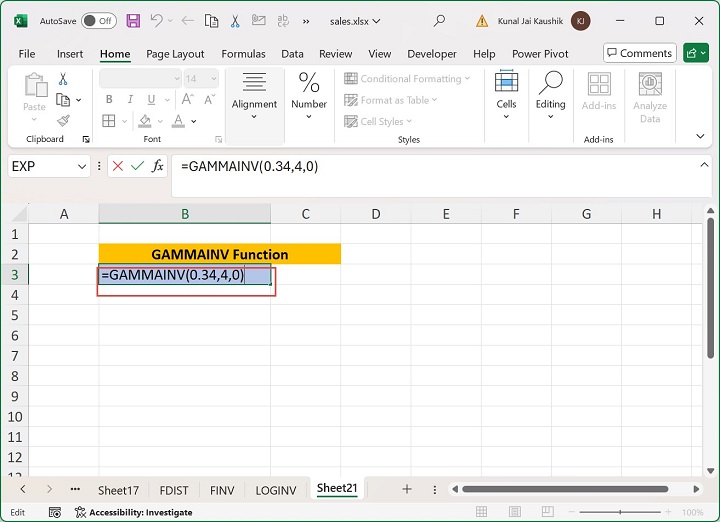
Once you press the Enter tab, the #NUM! error will be obtained.
Example 5
GAMMAINV function will retrieve the standard gamma distribution if the value of the Beta is equal to 1.
Solution
To accomplish this, you need to use GAMMA.DIST function. Here, you may enter the Beta value in the C8 cell. Now, write the formula =GAMMA.DIST(E5,C7,C8,TRUE) in the E9 cell and press the Enter tab.
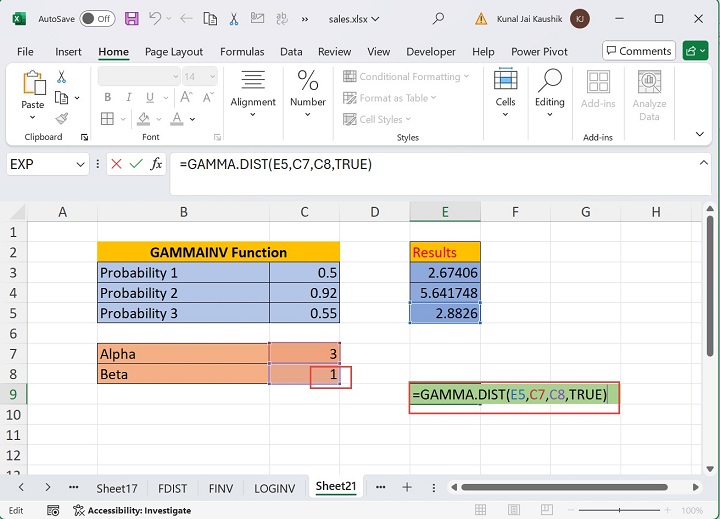
The resulting value is 0.55, the same as that of probability 3, which is 0.55, specified in the C5 cell.
