Fractional Part of a Circle

A complete or whole circle is taken as 1 and parts of the circles are represented as fractions. For example, if a circle is divided into 8 equal parts, each of the parts represents the fraction 1/8. Three parts of such a circle would represent 3/8 and on.
Here we are dealing with a type of problems, where fractions representing certain parts in a circle are given and we are required to find the fraction representing the remaining unknown part of the circle. To solve such problems, we add up the fractions representing the fractional parts and then subtract the sum from 1, the whole circle. The result gives the fraction representing the unknown fractional part of the circle.

How much of the circle is unshaded? Write your answer as a fraction in simplest form.

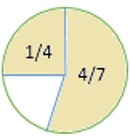
Solution

Step 1:

First we find what total part of figure is shaded.

$\frac{1}{4}$ + $\frac{4}{7}$ = $\frac{7}{28}$ + $\frac{16}{28}$ = $\frac{(7+16)}{28}$ = $\frac{23}{28}$

Step 2:

To find the fraction of the figure that is unshaded we subtract the result we got ($\frac{23}{28}$) from 1.

1 − $\frac{23}{28}$ = $\frac{28}{28}$ − $\frac{23}{28}$ = $\frac{(28−23}{28}$ = $\frac{5}{28}$

So, the fraction of the figure that is unshaded is $\frac{5}{28}$.

How much of the circle is shaded? Write your answer as a fraction in simplest form.

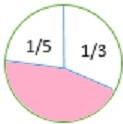
Solution

Step 1:

First we figure out how much of the figure is unshaded.

$\frac{1}{5}$ + $\frac{1}{3}$ = $\frac{3}{15}$ + $\frac{5}{15}$ = $\frac{(3+5)}{15}$ = $\frac{8}{15}$

Step 2:

To find the fraction of the figure that is unshaded we subtract the result we got ($\frac{8}{15}$) from 1.

1 − $\frac{8}{15}$ = $\frac{15}{15}$ − $\frac{8}{15}$ = $\frac{(15−8)}{15}$ = $\frac{7}{15}$

So, the fraction of the figure that is shaded is $\frac{7}{15}$.