
- Signals and Systems Tutorial
- Signals & Systems Home
- Signals & Systems Overview
- Signals Basic Types
- Signals Classification
- Signals Basic Operations
- Systems Classification
- Signals Analysis
- Fourier Series
- Fourier Series Properties
- Fourier Series Types
- Fourier Transforms
- Fourier Transforms Properties
- Distortion Less Transmission
- Hilbert Transform
- Convolution and Correlation
- Signals Sampling Theorem
- Signals Sampling Techniques
- Laplace Transforms
- Laplace Transforms Properties
- Region of Convergence
- Z-Transforms (ZT)
- Z-Transforms Properties
- Signals and Systems Resources
- Signals and Systems - Resources
- Signals and Systems - Discussion
Signals Sampling Theorem
Statement: A continuous time signal can be represented in its samples and can be recovered back when sampling frequency fs is greater than or equal to the twice the highest frequency component of message signal. i. e.
$$ f_s \geq 2 f_m. $$
Proof: Consider a continuous time signal x(t). The spectrum of x(t) is a band limited to fm Hz i.e. the spectrum of x(t) is zero for |ω|>ωm.
Sampling of input signal x(t) can be obtained by multiplying x(t) with an impulse train δ(t) of period Ts. The output of multiplier is a discrete signal called sampled signal which is represented with y(t) in the following diagrams:

Here, you can observe that the sampled signal takes the period of impulse. The process of sampling can be explained by the following mathematical expression:
$ \text{Sampled signal}\, y(t) = x(t) . \delta(t) \,\,...\,...(1) $
The trigonometric Fourier series representation of $\delta$(t) is given by
$ \delta(t)= a_0 + \Sigma_{n=1}^{\infty}(a_n \cos n\omega_s t + b_n \sin n\omega_s t )\,\,...\,...(2) $
Where $ a_0 = {1\over T_s} \int_{-T \over 2}^{ T \over 2} \delta (t)dt = {1\over T_s} \delta(0) = {1\over T_s} $
$ a_n = {2 \over T_s} \int_{-T \over 2}^{T \over 2} \delta (t) \cos n\omega_s\, dt = { 2 \over T_2} \delta (0) \cos n \omega_s 0 = {2 \over T}$
$b_n = {2 \over T_s} \int_{-T \over 2}^{T \over 2} \delta(t) \sin n\omega_s t\, dt = {2 \over T_s} \delta(0) \sin n\omega_s 0 = 0 $
Substitute above values in equation 2.
$\therefore\, \delta(t)= {1 \over T_s} + \Sigma_{n=1}^{\infty} ( { 2 \over T_s} \cos n\omega_s t+0)$
Substitute δ(t) in equation 1.
$\to y(t) = x(t) . \delta(t) $
$ = x(t) [{1 \over T_s} + \Sigma_{n=1}^{\infty}({2 \over T_s} \cos n\omega_s t) ] $
$ = {1 \over T_s} [x(t) + 2 \Sigma_{n=1}^{\infty} (\cos n\omega_s t) x(t) ] $
$ y(t) = {1 \over T_s} [x(t) + 2\cos \omega_s t.x(t) + 2 \cos 2\omega_st.x(t) + 2 \cos 3\omega_s t.x(t) \,...\, ...\,] $
Take Fourier transform on both sides.
$Y(\omega) = {1 \over T_s} [X(\omega)+X(\omega-\omega_s )+X(\omega+\omega_s )+X(\omega-2\omega_s )+X(\omega+2\omega_s )+ \,...] $
$\therefore\,\, Y(\omega) = {1\over T_s} \Sigma_{n=-\infty}^{\infty} X(\omega - n\omega_s )\quad\quad where \,\,n= 0,\pm1,\pm2,... $
To reconstruct x(t), you must recover input signal spectrum X(ω) from sampled signal spectrum Y(ω), which is possible when there is no overlapping between the cycles of Y(ω).
Possibility of sampled frequency spectrum with different conditions is given by the following diagrams:
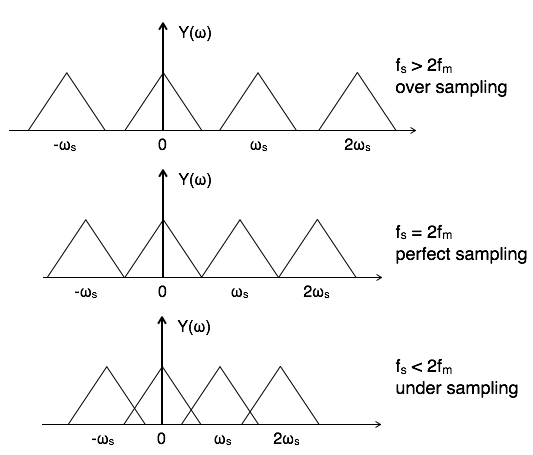
Aliasing Effect
The overlapped region in case of under sampling represents aliasing effect, which can be removed by
considering fs >2fm
By using anti aliasing filters.
