Electrical Transformer

---

---

In electrical and electronic systems, the electrical transformer is one of the most useful electrical machine. An electrical transformer can increase or decrease the magnitude of alternating voltage or current. It is the major reason behind the widespread use of alternating currents rather than direct current. A transformer does not have any moving part. Therefore, it has very high efficiency up to 99% and very strong and durable construction.

Electrical Transformer

A transformer or electrical transformer is a static AC electrical machine which changes the level of alternating voltage or alternating current without changing in the frequency of the supply.

A typical transformer consists of two windings namely primary winding and secondary winding. These two windings are interlinked by a common magnetic circuit for transferring electrical energy between them.

Principle of Transformer Operation

The operation of the transformer is based on the principle of mutual inductance, which states that when a changing magnetic field of one coil links to another coil, an EMF is induced in the second coil.

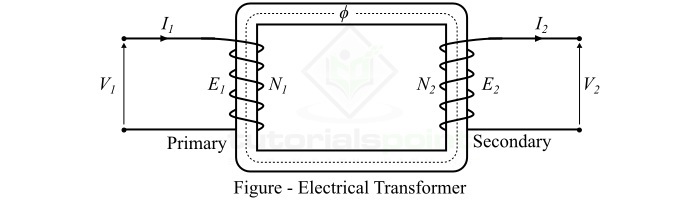
When an alternating voltage V₁ is applied to the primary winding, an alternating current flows through it and produces an alternating magnetic flux. This changing magnetic flux flows through the core of the transformer and links to the secondary winding. According to Faradays law of electromagnetic induction, an EMF E₂ is induced in the secondary winding due to the linkage of changing magnetic flux of the primary winding. If the secondary winding circuit is closed by connecting a load, then this induced EMF E₂ in the secondary winding causes a secondary current I₂ to flow through the load.

Although the changing magnetic flux of primary winding is also linked with the primary winding itself. Hence, an EMF E₁ is induced in the primary winding due to its own inductance effect. The value of E₁ and E₂ can be given by the following formulae,

$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:-\mathit{N_{\mathrm{1}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$

$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:-\mathit{N_{\mathrm{2}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$

Where N₁ and N₂ are the number of turns in the primary winding and secondary winding respectively.

On taking the ratio of E₂ and E₁, we get,

$$\mathrm{\frac{\mathit{E_{\mathrm{2}}}}{\mathit{E_{\mathrm{1}}}}\:=\:\frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}}$$

This expression is known as transformation ratio of the transformer. The transformation ratio depends on the number of turns in primary and secondary windings. Which means the magnitude of output voltage depends on the relative number of turns in primary and secondary windings.

If N₂ > N₁, then E₂ > E₁, i.e., the output voltage of the transformer is more than the input voltage, and such a transformer is known as set-up transformer. On the other hand, if N₁ > N₂, then E₁ > E₂ i.e., the output voltage is less than input voltage, such a transformer is called step-down transformer.

From the circuit diagram of the transformer, we can see that there is no electrical connection between the primary and secondary instead they are linked with the help of a magnetic field. Thus, a transformer enables us to transfer AC electrical power magnetically from one circuit to another which a change in the voltage and current level.

Types of Transformer

Based on operation, a transformer can be of the following three types −

• Step-up Transformer − Increases the voltage level from a lower voltage level.
• Step-down Transformer − Decreases the voltage level from a higher voltage level.
• Isolation Transformer − Does not change the voltage, but separates two electrical circuit electrically. It is also known as 1 to 1 transformer.

EMF Equation of Transformer

The mathematical expression that gives the value of induced EMF in windings of the transformer is known as emf equation of the transformer.

The EMF equation for primary winding is given by,

$$\mathrm{E_{1} \: = \: 4.44f \: \phi _{m}N_{1} \: = \: 4.44f \: B_{m}AN_{1}}$$

The EMF equation for secondary winding is given by,

$$\mathrm{E_{2} \: = \: 4.44f \: \phi _{m}N_{2} \: = \: 4.44f \: B_{m}AN_{2}}$$

Where, f is the supply frequency, m is the maximum flux in the core, Bm is the maximum flux density in the core, A is the area of cross-section of the core, ₁ and ₂ are the number of turns in the primary and secondary windings.

Turns Ratio of Transformer

The ratio of number of turns in the primary winding to the number of turns in the secondary winding of a transformer is referred to as turns ratio of the transformer. It is usually denoted by the symbol a.

$$\mathrm{Turns \: Ratio, a \: = \: \frac{Primary \: winding \: turns \: (N_{1})}{Secondary \: winding \: turns \: (N_{2})}}$$

Voltage Transformation Ratio of Transformer

The ratio of the output AC voltage to the input AC voltage of a transformer is known as the voltage transformer ratio of the transformer. It is usually denoted by the symbol K.

$$\mathrm{Voltage \: Transformation \: Ratio, \: K \: = \: \frac{Output \: Voltage \: (V_{2})}{Input \: Voltage \: (V_{1})}}$$

Current Transformation Ratio of Transformer

The ratio of the output current (secondary winding current) to the input current (primary winding current) of a transformer is known as current transformation ratio of the transformer.

$$\mathrm{Current \: Transformation \: Ratio, \: K \: = \: \frac{Secondary \: winding \: current \: (I_{2})}{Primary \: winding \: current \: (I_{1})}}$$

Relationship among Turns Ratio, Voltage Transformation Ratio, and Current Transformation Ratio

The relationship among turns ratio, voltage transformation ratio, and current transformation ratio is given by the following expression,

$$\mathrm{Turns \: Ratio, \: a \: = \: \frac{N_{1}}{N_{2}} \: = \: \frac{V_{1}}{V_{2}} \: = \: \frac{I_{2}}{I_{1}} \: = \: \frac{1}{K}}$$

Here, we can see that the current transformation is the reciprocal of the voltage transformation ratio. This is due to the fact that when a transformer increases the voltage, it reduces the current in the same proportion to maintain the constant MMF in the core.

MMF Equation of Transformer

MMF stands for Magnetomotive Force. The mmf is also referred to as ampere-turn rating of a transformer. The mmf is the driving force that establishes a magnetic flux in the core of a transformer. It is given by the product of number of turn in the winding and current through the winding.

For primary winding,

$$\mathrm{MMF \: = \: N_{1}I_{1}}$$

For secondary winding,

$$\mathrm{MMF \: = \: N_{2}I_{2}}$$

Where, I₁ and I₂ are the currents in primary and secondary windings of the transformer respectively.

Equivalent Resistance of Transformer Windings

The primary and secondary windings of a transformer are generally made up of copper wire. Thus, they have a finite resistance, although it is very small. The primary winding resistance is represented by R₁ and the secondary winding resistance is represented by R₂.

The equivalent resistance of transformer windings is given by referring the whole circuit of the transformer either on primary side or secondary side.

Thus, the equivalent resistance of transformer windings referred to primary side is given by,

$$\mathrm{R_{01} \: = \: R_{1} \: + \: R_{2}^{'} \: = \: R_{1} \: + \: \frac{R_{2}}{K^{2}}}$$

The equivalent resistance of transformer windings referred to secondary side is given by,

$$\mathrm{R_{02} \: = \: R_{2} \: + \: R_{1}^{'} \: = \: R_{2} \: + \: R_{1}K^{2}}$$

Where, R₁' is the primary winding resistance referred to secondary side, R₂' is the resistance of secondary winding referred to primary side, R₁ is the primary winding resistance, R₂ is the secondary winding resistance, R₀₁ is the equivalent resistance of transformer referred to primary side, and R₀₂ is the equivalent resistance of transformer referred to secondary side.

Leakage Reactance of Transformer Windings

The inductive reactance caused by the leakage magnetic flux in the transformer is referred to as the leakage reactance of the transformer windings.

For primary winding,

$$\mathrm{X_{1} \: = \: \frac{E_{1}}{I_{1}}}$$

For secondary winding

$$\mathrm{X_{2} \: = \: \frac{E_{2}}{I_{2}}}$$

Where, X₁ is the primary winding leakage reactance, X₂ is the secondary winding leakage reactance, E₁ is the self-induced emf in primary winding, and E₂ is the self-induced EMF in the secondary winding.

Equivalent Reactance of Transformer Windings

The equivalent reactance is the total reactance offered by both the primary and secondary windings of the transformer.

The equivalent reactance of transformer referred to primary side is,

$$\mathrm{X_{01} \: = \: X_{1} \: + \: X_{2}^{'} \: = \: X_{1} \: + \: \frac{X_{2}}{K^{2}}}$$

The equivalent reactance of transformer referred to secondary side is,

$$\mathrm{X_{02} \: = \: X_{2} \: + \: X_{1}^{'} \: = \: X_{2} \: + \: K^{2}X_{1}}$$

Where, X₁' is the leakage reactance of primary winding on secondary side, X₂' is the leakage reactance of secondary winding on primary side.

Total Impedance of Transformer Windings

The combined opposition offered by the winding resistances and leakage reactances is referred to as the total impedance of the transformer windings.

The impedance of the primary winding of transformer is,

$$\mathrm{Z_{1} \: = \: \sqrt{R_{1}^{2} \: + \: X_{1}^{2}}}$$

The impedance of the secondary winding of transformer is,

$$\mathrm{Z_{2} \: = \: \sqrt{R_{2}^{2} \: + \: X_{2}^{2}}}$$

The equivalent impedance of transformer referred to primary side is given by,

$$\mathrm{Z_{01} \: = \: \sqrt{R_{01}^{2} \: + \: X_{01}^{2}}}$$

The equivalent impedance of transformer referred to secondary side is given by,

$$\mathrm{Z_{02} \: = \: \sqrt{R_{02}^{2} \: + \: X_{02}^{2}}}$$

Input and Output Voltage Equations of Transformer

The input and output voltage equations of a transformer are found using KVL in the equivalent circuit of the transformer.

The input voltage equation of a transformer is given by,

$$\mathrm{V_{1} \: = \: E_{1} \: + \: I_{1}R_{1} \: + \: jI_{1}X_{1} \: = \: E_{1} \: + \: I_{1} ( R_{1} \: + \: jX_{1} ) \: = \: E_{1} \: + \: I_{1}Z_{1}}$$

The output voltage equation of a transformer is given by,

$$\mathrm{V_{2} \: = \: E_{2} \: - \: I_{2}R_{2} \: - \: jI_{2}X_{2} \: = \: E_{2} \: - \: I_{2} ( R_{2} \: + \: jX_{2} ) \: = \: E_{2} \: - \: I_{2}Z_{2}}$$

Transformer Losses

There are two types of losses occur in a transformer − core loss and copper loss.

Core Losses of Transformer

The total core loss of the transformer is the sum of hysteresis loss and eddy current loss, i.e.,

$$\mathrm{Core \: loss \: = \: P_{h} \: + \: P_{e}}$$

Where, the hysteresis loss is caused due to magnetic reversal in the core.

$$\mathrm{Hysteresis \: loss, \: P_{h} \: = \: \eta B_{max}^{1.6}fV}$$

And, the eddy current occurs due to eddy currents flowing in the core.

$$\mathrm{Eddy \: current\: loss, \: P_{e} \: = \: k_{e} B_{m}^{2}f^{2}t^{2}}$$

Where, η is the Steinmetz coefficient, B_m is the maximum flux density in the core, K_e is the eddy current constant, f is the frequency of magnetic flux reversal, V is the volume of core.

Copper Loss of Transformer

The copper loss occurs due to resistance of the transformer windings.

$$\mathrm{Copper \: loss \: = \: I_{1}^{2}R_{1} \: + \: I_{2}^{2}R_{2}}$$

Voltage Regulation of Transformer

The voltage regulation of transformer is defined as the change in output voltage from no-load to full load with respect to the no-load voltage.

$$\mathrm{Voltage \: Regualation \: = \: \frac{No \: load \: voltage \: - \: Full\: load\: voltage}{No \: load\: voltage}}$$

Transformer Efficiency

The ratio of the output power to the input power is called the efficiency of the transformer.

$$\mathrm{Efficiency, \: \eta \: = \: \frac{Output \: power \: ( P_{o} )}{Input \: power \: ( P_{i} )}}$$

$$\mathrm{Efficiency, \: \eta \: = \: \frac{Output \: power}{Output \: power \: + \: Losses}}$$

Transformer Efficiency at Any Load

The efficiency of transformer at an actual load is calculated using the following formula,

$$\mathrm{\eta \: = \: \frac{x \: \times \: full \: load \: k VA \: \times \: power \: factor}{ (x \: \times \: full \: load \: kVA \: \times \: power \: factor )+Losses}}$$

Where, x is the fraction of loading.

All Day Efficiency of Transformer

The all-day efficiency of a transformer is defined as the ratio of output energy in kWh to the input energy in kWh recorded for 24 hours

$$\mathrm{\eta_{allday} \: = \: \frac{Output \: energy \: in \: kWh}{Input \: energy \: in \: kWh}}$$

Condition for Maximum Efficiency of Transformer

When the core losses and copper losses of a transformer are equal, the transformer efficiency is maximum.

Thus, for maximum efficiency of transformer,

$$\mathrm{Copper \: loss \: = \: Core\: loss}$$

Load Current Corresponding to Maximum Efficiency of Transformer

The load current or secondary winding current for the maximum efficiency of a transformer is given by,

$$\mathrm{I_{2} \: = \: \sqrt{\frac{P_{i}}{R_{02}}}}$$

Important Points

Note the following important points about transformers −

• The operation of transformer is based on the principle of electromagnetic induction.
• The transformer does not change the frequency, i.e. the frequency of input supply and output supply remains the same.
• Transformer is a static electrical machine, which means it does not have any moving part. Hence, it has very high efficiency.
• Transformer cannot work with direct current because it is an electromagnetic induction machine.
• There is no direct electrical connection between primary and secondary windings. The AC power is transferred from primary to secondary through magnetic flux.