Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Voltage and Currents in Star and Delta Connected Systems
Star (Wye) Connected System
Let VR, VY and VB represents the three phase voltages while VRY, VYB and VBR represents the line voltages. Assume that the system is balanced, so
$$\mathrm{\lvert\:V_{R}\rvert=\lvert\:V_{Y}\rvert=\lvert\:V_{B}\rvert=\lvert\:V_{ph}\rvert}$$
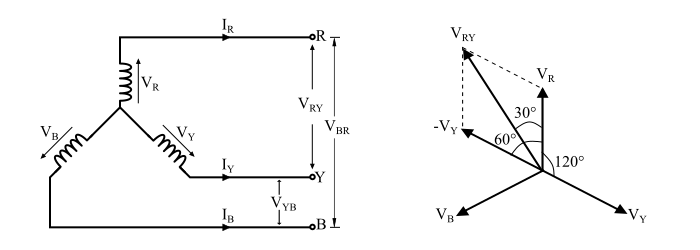
From the circuit and phasor diagram of star connected load, it can be observed that the line voltage VRY is a vector difference of VR and VY or the vector sum of VR and –VY, i.e.
$$\mathrm{V_{RY}=V_{R}+(-V_{Y})=V_{R}-V_{Y}}$$
Applying parallelogram law to obtain the magnitude of this, we get,
$$\mathrm{V_{RY}=\sqrt{V_R^2+V_Y^2+2V_RV_{Y}\cos\:60^{\circ}}}$$
$$\mathrm{\Rightarrow\:V_{RY}=\sqrt{V_{ph}^2+V_{ph}^2+2V_{ph}^2\cos\:60^{\circ}}=\sqrt{3}V_{ph}}$$
Similarly,
$$\mathrm{V_{YB}=V_{Y}-V_{B}=\sqrt{3}V_{ph}}$$
$$\mathrm{V_{BR}=V_{B}-V_{R}=\sqrt{3}V_{ph}}$$
$$\mathrm{\because\:V_{RY}=V_{YB}=V_{BR}=V_{L}=Line\:Voltage}$$
$$\mathrm{\therefore\:V_{L}=\sqrt{3}V_{ph}}$$
Therefore, in a star connected system,
Line Voltage = √3 × Phase Voltage
Again, refer the circuit of star connected system, it can be seen that each line is in series with its individual phase winding. Therefore, in a star connection, the line current in each line is equal to the current in the corresponding phase winding.
Let IR, IY and IB being the currents in R, Y and B lines respectively. Since, the load is balanced, therefore,
$$\mathrm{I_{R}=I_{Y}=I_{B}=I_{ph}(say)}$$
Then,
$$\mathrm{I_{L}=I_{ph}}$$
⇒Line Current = Phase Current
Note – for a balanced star connected system, the vector sum of line current is equal to zero,
i.e.
$$\mathrm{I_{R}+I_{Y}+I_{B}=I_{n}=0}$$
Where, In is the neutral current.
Delta Connected System
Let IRY, IYB and IBR are the phase current in delta connected system while IR, IY and IB being the line currents.
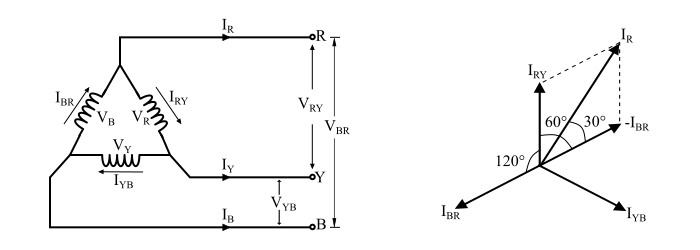
By referring the circuit and phasor diagram, it can be seen that current in each line is the vector difference of corresponding phase currents and are given as,
$$\mathrm{I_{R}=I_{BR}-I_{RY}}$$
$$\mathrm{I_{Y}=I_{RY}-I_{YB}}$$
$$\mathrm{I_{B}=I_{YB}-I_{BR}}$$
Now, the magnitude of current IR can be obtained by parallelogram law of vector addition, as follows,
$$\mathrm{I_{R}=\sqrt{I_{BR}^{2}+I_{RY}^2+2I_{BR}I_{RY}\cos\:60^{\circ}}}$$
Assume the system is balanced, therefore,
$$\mathrm{\lvert\:I_{RY}\rvert=\lvert\:I_{BR}\rvert=\lvert\:I_{YB}\rvert=I_{ph}}$$
$$\mathrm{\Rightarrow\:I_{R}=\sqrt{I_{ph}^{2}+I_{ph}^2+2I_{ph}^2\cos\:60^{\circ}}=\sqrt{3}I_{ph}}$$
Similarly,
$$\mathrm{I_{Y}=\sqrt{3}I_{ph}\:\:and\:\:I_{B}=\sqrt{3}I_{ph}}$$
Since the system is balanced, therefore the current through each line will be the same, i.e.
$$\mathrm{I_{R}=I_{Y}=I_{B}=I_{L}=Line\:Current}$$
$$\mathrm{\therefore\:I_{L}=\sqrt{3}\:I_{ph}}$$
$$\mathrm{\Rightarrow\:Line\:Current=\sqrt{3}\times\:Phase\:Current}$$
Since, neutral does not exist in a delta connected system, thus the phase voltage and line voltage are same. Refer the circuit diagram,
$$\mathrm{V_{RY}=V_{YB}=V_{BR}=V_{L}}$$
$$\mathrm{\Rightarrow\:V_{L}=V_{ph}}$$
12K+ Views
