Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Step Response of Series RLC Circuit using Laplace Transform
Laplace Transform
The Laplace transform is a mathematical tool which is used to convert the differential equation in time domain into the algebraic equations in the frequency domain or s-domain.
Mathematically, if $\mathrm{\mathit{x\left ( t \right )}}$ is a time domain function, then its Laplace transform is defined as −
$$\mathrm{\mathit{L\left [ x\left ( t \right ) \right ]\mathrm{\mathrm{=}}X\left ( s \right )\mathrm{\mathrm{=}}\int_{-\infty }^{\infty }x\left ( t \right )e^{-st}\; dt\; \; \; \cdot \cdot \cdot \left ( \mathrm{1} \right )}}$$
Also, the inverse Laplace transform of the function is defined as,
$$\mathrm{\mathit{L^{-\mathrm{1}}\left [X\left ( s \right ) \right ]\mathrm{\mathrm{=}}x\left ( t \right ) \mathrm{\mathrm{=}}\int_{\sigma -j\infty }^{\sigma \mathrm{\: +\: }j\infty }X\left ( s \right )e^{st}\; ds\; \; \; \cdot \cdot \cdot \left ( \mathrm{2} \right )}} $$
Step Response of Series RLC Circuit
A series RLC circuit is shown in Figure-1.
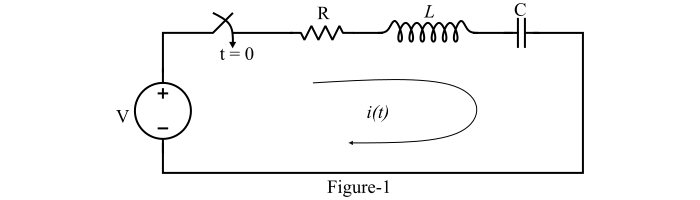
The equation describing this system is given as,
$$\mathrm{\mathit{Vu\left ( t \right )\mathrm{\mathrm{=}}Ri\left ( t \right )\mathrm{\: +\: }L\frac{di\left ( t \right )}{dt}\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{t}i\left ( t \right )dt}}$$
$$\mathrm{\Rightarrow \mathit{Vu\left ( t \right )\mathrm{\mathrm{=}}Ri\left ( t \right )\mathrm{\: +\: }L\frac{di\left ( t \right )}{dt}\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt\; \; \cdot \cdot \cdot \left ( \mathrm{3} \right )}}$$
Taking Laplace transform of equation (3) on both sides, we get,
$$\mathrm{\mathit{\mathrm{\textbf{L}}\left [ Vu\left ( t \right ) \right ]\mathrm{\mathrm{=}}\mathrm{\textbf{L}}\left [ Ri\left ( t \right ) \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ L\frac{di\left ( t \right )}{dt} \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ \frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ \frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt \right ]}} $$
$$\mathrm{\mathit{\Rightarrow \frac{V}{s}\mathrm{=}RI\left ( s \right )\mathrm{\: +\: }L\left [ sI\left ( s \right )-i\left ( \mathrm{0^{\mathrm{\: +\: }}} \right ) \right ]\mathrm{\: +\: }\frac{\mathrm{1}}{C}\mathrm{\textbf{L}}\left [ q\left ( \mathrm{0^{\mathrm{\: +\: }}} \right ) \right ]\mathrm{\: +\: }\frac{\mathrm{1}}{C}\frac{I\left ( s \right )}{s}\; \; \cdot \cdot \cdot \left ( \mathrm{4} \right )}}$$
Where,
$\mathrm{\mathit{i\left ( \mathrm{0}^{\mathrm{ + }} \right )}}$ is the initial current through the inductor, and
$\mathrm{\mathit{q\left ( \mathrm{0}^{\mathrm{ + }} \right )}}$ is the initial charge on the capacitor.
By neglecting the initial conditions of inductor and capacitor, we can write the equation (4) as,
$$\mathrm{\mathit{\frac{V}{s}\mathrm{\mathrm{=}}RI\left ( s \right )\mathrm{\: +\: }LsI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\frac{I\left ( s \right )}{s}}}$$
$$\mathrm{\Rightarrow \mathit{\frac{V}{s}\mathrm{\mathrm{=}}\left ( R\mathrm{\: +\: }sL\mathrm{\: +\: }\frac{\mathrm{1}}{sC} \right )I\left ( s \right )\; \; \cdot \cdot \cdot \left ( \mathrm{5} \right )}} $$
Therefore, the current through the circuit is given by,
$$\mathrm{ \mathit{I\left ( s \right )\mathrm{\mathrm{=}}\frac{V}{\left ( sR\mathrm{\: +\: }s^{\mathrm{2}}L\mathrm{\: +\: }\frac{\mathrm{1}}{C} \right )}\; \; \cdot \cdot \cdot \left ( \mathrm{6} \right )}} $$
Also,
$$\mathrm{ \mathit{I\left ( s \right )\mathrm{\mathrm{=}}\frac{V}{L\left [ s^{\mathrm{2}}\mathrm{\: +\: }\left ( \frac{R}{L} \right )s\mathrm{\: +\: }\frac{\mathrm{1}}{LC} \right ]}\mathrm{=}\frac{V}{L\left ( s-a_{\mathrm{1}} \right )\left ( s-a_{\mathrm{2}} \right )}\; \; \cdot \cdot \cdot \left ( \mathrm{7} \right )}}$$
Where, $\mathrm{\mathit{a_{\mathrm{1}}}}$ and $\mathrm{\mathit{a_{\mathrm{2}}}}$ are the roots of the equation $\mathrm{ \mathit{\left [ s^{\mathrm{2}}\mathrm{\: +\: }\left ( \frac{R}{L} \right )s\mathrm{\: +\: }\frac{\mathrm{1}}{LC} \right ]}}$ and are given by,
$$\mathrm{ \mathit{a_{\mathrm{1}},a_{\mathrm{2}}\mathrm{=}-\frac{R}{\mathrm{2}L}\pm\frac{\mathrm{1}}{\mathrm{2}L}\sqrt{R^{\mathrm{2}}-\frac{\mathrm{4}L}{C}}\; \; \cdot \cdot \cdot \left ( \mathrm{8} \right )}}$$
Now, by taking the inverse Laplace transform of the equation (8), we obtain the current as the function of time, i.e.,
$$\mathrm{ \mathit{i\left ( t \right )\mathrm{=}L^{-\mathrm{1}}\left [ I\left ( s \right ) \right ]\mathrm{=}L^{-\mathrm{1}}\left [ \frac{V}{L\left ( s-a_{\mathrm{1}} \right )\left ( s-a_{\mathrm{2}} \right )} \right ] }}$$
$$\mathrm{ \mathit{i\left ( t \right )\mathrm{=}\frac{V}{L\left ( a_{\mathrm{1}}-a_{\mathrm{2}} \right )}\left [ e^{a_{\mathrm{1}}t} - e^{a_{\mathrm{2}}t}\right ]\; \; \cdot \cdot \cdot \left ( \mathrm{9} \right )}}$$
Equation (9) is the step response of the series RLC circuit.
Numerical Example
Find the current in the series RLC circuit shown in Figure-2.
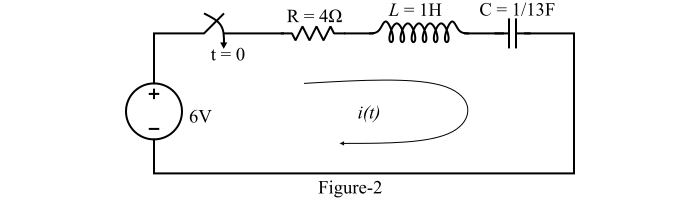
Solution
The KVL equation describing the given series RLC circuit is,
$$\mathrm{\mathit{\mathrm{6}u\left ( t \right )\mathrm{\mathrm{=}}Ri\left ( t \right )\mathrm{\: +\: }L\frac{di\left ( t \right )}{dt}\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt}}$$
Taking the Laplace transform of the above equation on both sides, we get,
$$\mathrm{\mathit{\mathrm{\textbf{L}}\left [ \mathrm{6}u\left ( t \right ) \right ]\mathrm{\mathrm{=}}\mathrm{\textbf{L}}\left [ Ri\left ( t \right ) \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ L\frac{di\left ( t \right )}{dt} \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ \frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt \right ]}}$$
$$\mathrm{\Rightarrow \mathit{\frac{\mathrm{6}}{s}\mathrm{\mathrm{=}}RI\left ( s \right )\mathrm{\: +\: }sLI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{sC}I\left ( s \right )}} $$
Substituting the values of R, L and C, we obtain,
$$\mathrm{\mathit{\frac{\mathrm{6}}{s}\mathrm{\mathrm{=}}\mathrm{4}I\left ( s \right )\mathrm{\: +\: }sI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{13}}{s}I\left ( s \right )}}$$
$$\mathrm{\Rightarrow \mathit{\left ( s^{\mathrm{2}}\mathrm{\: +\: }\mathrm{4}s\mathrm{\: +\: }\mathrm{13} \right )I\left ( s \right )\mathrm{=}\mathrm{6}}}$$
$$\mathrm{\therefore \mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{6}}{\left ( s^{\mathrm{2}}\mathrm{\: +\: }\mathrm{4}s\mathrm{\: +\: }\mathrm{13} \right )}\mathrm{=}\frac{\mathrm{6}}{\left ( s\mathrm{\: +\: 2} \right )^{\mathrm{2}}\mathrm{\: +\: }\mathrm{3^{2}}}}}$$
$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{6}}{\mathrm{3}}\left [ \frac{\mathrm{3}}{\left ( s\mathrm{\: \mathrm{\: +\: } \: 2} \right )^{\mathrm{2}}\mathrm{\: +\: }\mathrm{3^{2}}} \right ]}}$$
By taking the inverse Laplace transform, we get,
$$\mathrm{ \mathit{i\left ( t \right )\mathrm{=}L^{-\mathrm{1}}\left [ I\left ( s \right ) \right ]\mathrm{=}\frac{\mathrm{6}}{\mathrm{3}}L^{-\mathrm{1}}\left [ \frac{\mathrm{3}}{\left ( s\mathrm{\: \mathrm{\: +\: } \: 2} \right )^{\mathrm{2}}\mathrm{\: +\: }\mathrm{3^{2}}} \right ]}} $$
$$\mathrm{ \therefore \mathit{i\left ( t \right )\mathrm{=}\mathrm{2}e^{-\mathrm{2}t}\: \mathrm{sin\, 3}t\: u\left ( t \right )}}$$
11K+ Views
