Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Fourier Transform of Signum Function
Fourier Transform
The Fourier transform of a continuous-time function $x(t)$ can be defined as,
$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt}$$
Fourier Transform of Signum Function
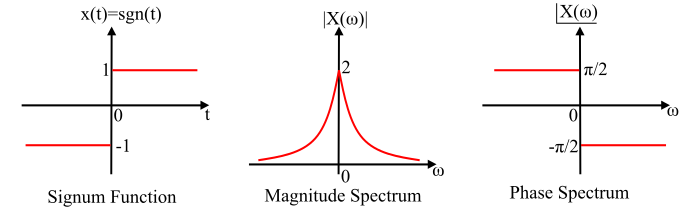
The signum function is represented by $sgn(t)$ and is defined as
$$\mathrm{sgn(t)=\begin{cases}1 & for\:t>0\-1 & for\:t<0 \end{cases}}$$
As the signum function is not absolutely integrable. Hence, its Fourier transform cannot be found directly. Therefore, to find the Fourier transform of the signum function, consider the function as given below.
$$\mathrm{x(t)=e^{-a|t|}sgn(t);\:\:a\rightarrow 0}$$
Therefore, the signum function can be obtained as,
$$\mathrm{x(t)=sgn(t)=\lim_{a\rightarrow \:0}e^{-a|t|}sgn(t)}$$
$$\mathrm{\Rightarrow\:x(t)=\lim_{a\rightarrow \:0}[e^{-at}u(t)-e^{at}u(-t)]}$$
From the definition of the Fourier transform, we have,
$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}\:dt=\int_{−\infty}^{\infty}sgn(t)e^{-j\omega t}\:dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{−\infty}^{\infty}\left(\lim_{a\rightarrow \:0}[e^{-at}u(t)-e^{at}u(-t)] \right)e^{-j\omega t}\:dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left[\int_{−\infty}^{\infty}e^{-at}e^{-j\omega t}u(t)dt- \int_{−\infty}^{\infty}e^{at}e^{-j\omega t}u(-t)dt\right]}$$
$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left[\int_{0}^{\infty}e^{-(a+j\omega)t}dt- \int_{−\infty}^{0}e^{(a-j\omega)t}dt\right]}$$
$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left[\int_{0}^{\infty}e^{-(a+j\omega)t}dt- \int_{0}^{\infty}e^{-(a-j\omega)t}dt\right]}$$
$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left\{\left[\frac{e^{-(a+j\omega)t}}{-(a+j\omega)}\right]_{0}^{\infty} -\left[\frac{e^{-(a-j\omega)t}}{-(a-j\omega)}\right]_{0}^{\infty}\right \}}$$
$$\mathrm{\Rightarrow\:X(\omega)=\lim_{a\rightarrow \:0}\left\{\left[\frac{e^{-\infty}-e^{0}}{-(a+j\omega)} \right]- \left[\frac{e^{-\infty}-e^{0}}{-(a-j\omega)} \right] \right\}}$$
$$\mathrm{=\lim_{a\rightarrow \:0}\left[ \frac{1}{(a+j\omega)}-\frac{1}{(a-j\omega)}\right]}$$
On solving the limits, we get,
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{j\omega}-\frac{1}{(-j\omega)}=\frac{2}{j\omega}}$$
Therefore, the Fourier transform of the signum function is,
$$\mathrm{X(\omega)=F[sgn(t)]=\frac{2}{j\omega}}$$
Or, it can also be represented as,
$$\mathrm{sgn(t)\overset{FT}{\leftrightarrow}\frac{2}{j\omega}}$$
The magnitude and phase representation of Fourier transform of the Signum function −
$$\mathrm{Magnitude, |X(\omega)| =\sqrt{0+\left(\frac{2}{\omega}\right)^{2}}=\frac{2}{\omega};\:\:for\:all\:\omega}$$
$$\mathrm{Phase,\angle\:X(\omega) =\begin{cases}\frac{\pi}{2}; & for\:\omega<0 \ -\frac{\pi}{2}; & for\:\omega>0 \end{cases}}$$
The graphical representation of the signum function with its magnitude and phase spectra is shown in the figure below.
16K+ Views
